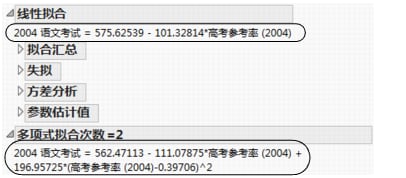
“拟合汇总”报表显示针对相同数据的线性拟合和二次多项式拟合的响应的数值汇总。您可以比较多个“拟合汇总”报表,通过观察 R 方值是否增大,均方根误差是否减小来判断不同模型之间是否有改进。
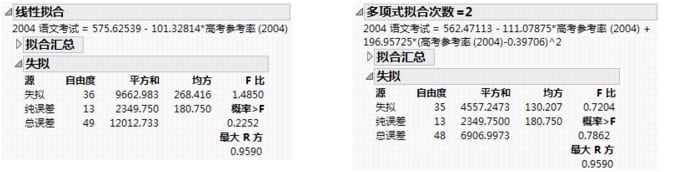
使用“失拟”报表,无论您的模型形式是否正确,您都可以估计误差。当多个观测具有相同的 x 值时就会出现这种误差。为这些精确重复测量的误差称为纯误差。这是样本误差中无论使用哪种形式的模型都无法解释或预测的部分。不过,若失拟检验中的自由度不高(重复的 x 值不多),则失拟检验的用处不大。
模型剩余误差与纯误差之间的差值称为失拟误差。若回归变量的函数形式有误,则失拟误差可能显著大于纯误差。这种情况下,应该尝试不同类型的模型拟合。“失拟”报表检验失拟误差是否为零。
每种误差来源的自由度 (DF)。
|
‒
|
|
‒
|
平方和除以与其相关的自由度。该计算将平方和转换为平均值(均方)。用于统计检验的 F 比是均方之比。
|
‒
|
|
‒
|
|
‒
|
|
‒
|
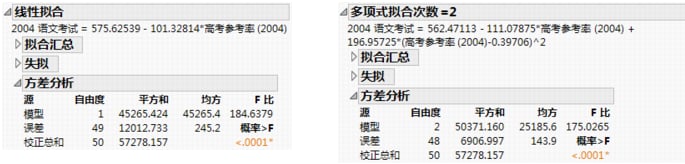
在本例中,每个响应与样本均值之间距离的总平方和(校正总和)为 57,278.157,如线性拟合和多项式拟合的“方差分析”报表的示例所示。 这是用于与其他所有模型进行比较的基本模型(或简单均值模型)的平方和。
|
|
‒
|
对于线性回归,每个点与拟合线之间距离的平方和减至 12,012.733。这是在拟合模型后剩余或未解释的(误差)平方和。二次多项式拟合的剩余平方和为 6,906.997,该拟合比线性拟合所解释的变异略多一些。也就是说,该模型可解释更多变异,因为二次多项式的模型平方和比线性拟合的模型平方和要高。校正总和平方和减去误差平方和之后的值就是模型平方和。
|
平方和除以与其相关的自由度。用于统计检验的 F 比是以下均方的比值:
|
‒
|
线性拟合的模型均方为 45,265.4。该值估计误差方差,但仅是在模型参数为零的假设前提之下。
|
|
‒
|
误差均方为 245.2。该值估计误差方差。
|
模型均方除以误差均方。该拟合的假设前提是所有回归参数(截距除外)都为零。若该假设成立,则误差均方和模型均方都估计误差方差,并且它们的比值服从 F 分布。若某个参数是显著的模型效应,则 F 比通常仅在随机情况下高于预期值。
列出从每个 t 比计算得出观测到的显著性概率。它是随机得到 t 比的绝对值大于计算值的概率(在原假设成立的前提下)。通常将 0.05(或有时为 0.01)以下的值解释为参数与零之间存在显著差异的证据。
要显示其他统计量,请在报表中右击并选择列菜单。默认情况下不显示的统计量如下所示:
|
•
|
|
•
|