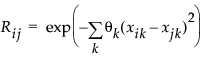但是,正如双因子的拉丁超立方设计 中的示例所示,拉丁超立方设计可能不能为您提供最优空间填充属性。该示例是双因子 16 次试验的拉丁超立方设计,它将因子水平设置在 -1 到 1 之间。双因子图显示该设计具有缺失覆盖的区域。特别是对接近 0 的 X1 和接近 -1 的 X2 覆盖很差。
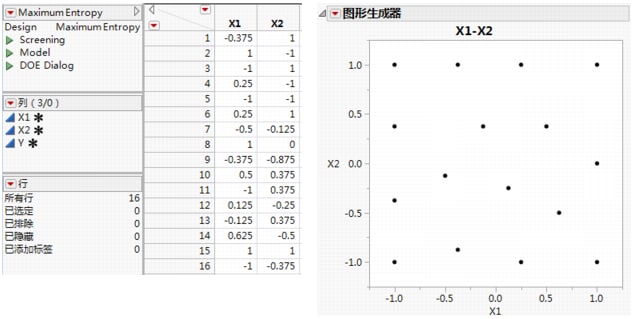
最大熵设计是针对计算机实验的拉丁超立方设计的备选设计。最大熵设计优化了实验中所含信息量的测量。请参见下面的技术说明。将因子水平设置在 -1 到 1 之间,双因子最大熵设计 中所示的双因子最大熵设计比双因子的拉丁超立方设计 中所示的拉丁超立方设计更好地覆盖了该区域。当试验次数增加时,设计的空间填充属性会改善。
技术说明:假定数据来自正态 (m, s2 R) 分布,最大熵设计使实验的 Shannon 信息(Shewry 和 Wynn (1987))最大化,其中
是两个不同设计点 xi 和 xj 上响应值的相关性。在计算上而言,这些设计使 |R|(样本的相关性矩阵的行列式)最大化。若 xi 和 xj 相距很远,则 Rij 接近于 0。若 xi 和 xj 相距很近,则 Rij 接近于 1。