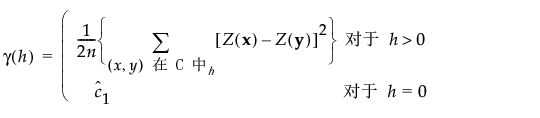拟合线性模型 • 混合模型 • 统计详细信息 • 空间和时间变异性
上一个
 • 
下一个
空间和时间变异性
考虑简单模型 。 通过误差项 ei 对空间或时间结构建模。通常，空间相关性模型可以定义为 且 。
用 si 表示 yi 的位置，其中通过反映空间或时间的坐标指定 si。通常通过假定协方差是欧几里得距离 dij（si 和 sj 之间）的函数，限制空间或时间结构。该协方差可以表示为 ，其中 表示观测值 yi 和 yj 之间的相关性。
在两个或更多位置坐标的情况下，若 f(dij) 不依赖于方向，则协方差结构为各向同性。若依赖于方向，则该结构为各向异性。
空间相关性结构
下面显示 JMP 中可用的空间模型的相关性结构。这些结构由参数 ρ 表示，除非另行约束，否则该参数值为正数。
•
球形
其中
•
指数
•
高斯
•
乘方
对于各向异性模型，相关性函数针对每个方向包含一个参数 ρκ。
变差图
当空间过程为二阶平稳时，空间相关性结构中列出的结构定义变差图。从地质统计学借鉴而来，变差图是用于描述和估计空间变异性的标准工具。它使用半方差测量作为两个观测值之间的距离 dij 的函数的空间变异性。
用 Z(s) 表示位置 s 处的响应值。按以下方式给出 si 和 sj 处的两个观测值之间的半方差：
若响应具有常数均值，则表达式可以简化为：
若过程是各向同性的，则半方差仅依赖于两个点之间的距离 h 且函数可以表示为：
以下项与变差图关联：
Nugget
定义为截距。它表示 h = 0 处的跳跃不连续性。
Sill
定义为在达到更大距离的平稳值处的半变差图的值。它对应于观测值的方差。在不带 nugget 效应的模型中，sill 为 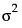。在带 nugget 效应的模型中，sill 为 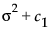，其中 c1 表示 nugget。偏 sill 定义为 。
极差
定义为半变差图达到 sill 处的距离。在小于极差的距离处，观测值在空间上是相关的。对于大于等于极差的距离，空间相关性实际上为零。在球形模型中，ρ 为极差。在指数模型中，3ρ 为实际极差。在高斯模型中， 为实际极差。实际极差定义为协方差下降到 95% 的 sill 处的距离。
在“拟合混合模型”报表 - 带 Nugget 的空间球体中，重复效应协方差参数估计值表示各种半变差图功能：
空间球体
极差 ρ 的估计值。
Nugget
的统一尺度的估计值。残差与 Nugget 之积为 。
残差
偏 sill 或无 nugget 模型中的 sill。
变差图估计值
对于给定的各向同性空间结构，使用非线性最小二乘法将观测数据拟合为空间相关性结构中的合适函数，以得到估计的变差图。
经验半方差
要计算经验半方差，需要计算为变差图协方差选择的变量的所有点对之间的距离。距离的极差分为 10 个相等的区间。若数据不允许 10 个区间，则构造尽可能多的区间。
构造包含点对的距离分类。第 h 个距离分类包含其距离位于第 h 个区间的所有点对。
采用以下符号：
n
点对总数
Ch
包含其距离位于第 h 个最大区间的点的距离分类
Z(x)
x 处的响应值，其中 x 是时间或空间坐标的向量
g(h)
距离分类 Ch 的半方差
按以下方式定义半方差函数 γ：
在此 是 nugget 效应的估计值。