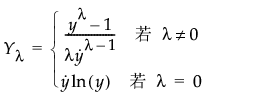拟合线性模型 • 标准最小二乘报表和选项 • 因子刻画 • Box-Cox Y 变换
上一个
 • 
下一个
Box-Cox Y 变换
Box-Cox 幂变换用于变换响应，以便能够更接近于满足通常的正态性和方差齐性回归假设。变换响应随后可以使用回归模型进行拟合。不过，您还可能出于其他原因使用 Box-Cox 幂变换来变换变量。仅当响应 Y 为严格正数时，这种变换才适用。
常用的变换是将响应升高到特定次幂。Box and Cox (1964) 对这一系列的幂变换进行了规范化和说明。构造该变换的公式以便按照参数 λ 提供连续定义，这样即可比较误差平方和。具体而言，以下方程提供了一系列的变换：
在此， 表示几何均值。
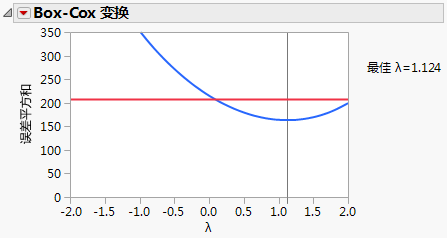
“Box-Cox Y 变换”选项对从 λ = –2 到 2（增量为 0.2）的变换进行拟合。要选择适当的 λ 值，将为这些变换中的每一个变换计算似然函数。计算的假设前提是：误差是独立的，服从均值为 0 且方差为 σ2 的正态分布。将选择使似然函数最大化的 λ 值。该值还使误差平方和在 λ 的选定值中最小。
“Box-Cox 变换”报表显示一个图，其中显示 λ 的值与误差平方和 (SSE) 的对应关系。
“Box-Cox 变换”报表提供以下选项：
使用变换重新拟合
支持您指定 lambda 值以定义变换的 Y 变量，之后提供变换后的变量的最小二乘拟合。
使用变换替换
支持您指定 lambda 值以定义变换的 Y 变量，之后使用变换后变量的拟合替换当前的最小二乘拟合。若有多重响应，“使用变换替换”仅替换您所变换的响应的报表。
保存最佳变换
在数据表中创建一个新列并保存最佳变换的公式。
保存特定变换
支持您指定 lambda 值，并使用您指定的变换的公式在数据表中创建列。
估计值表
创建一个新的数据表，其中包含从 –2 到 2（以 0.2 为增量）的所有 λ 的参数估计值和误差平方和值。
“Box-Cox Y 变换”的示例
1.
选择帮助 > 样本数据库，然后打开 Reactor.jmp。
2.
选择分析 > 拟合模型。
3.
选择 Y 并点击 Y。
4.
确保次数框的值为 2。
5.
选择 F、Ct、A、T 和 Cn，然后点击宏 > 析因次数。
6.
点击运行。
Box-Cox Y 变换
该图显示 λ 的最佳值大约介于 1.0 到 1.2 之间。JMP 选择的值（以 0.2 个单位的 λ 值为增量）为 1.124。
7.
（可选）要查看用于构造图形的误差平方和值，请选择估计值表。