除“使用修改 MLE 的 Crow-AMSAA”选项外,λ 和 β 的估计值是最大似然估计值,它们按如下方式进行计算。使用 Meeker and Escobar (1998) 中的方法得到的该似然函数。它根据 param1 = log(λ) 和 param2 = log(β) 重新进行了参数化。这样就可以使用不受约束的优化算法,即在 -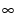 到 +
到 + 范围上进行搜索的算法。 此外还会得到 param1 和 param2 的 MLE。
范围上进行搜索的算法。 此外还会得到 param1 和 param2 的 MLE。
λ 和 β 的标准误差根据 Fisher 信息矩阵获得。使用 Wald 统计量基于 MLE 的渐近分布计算 param1 和 param2 的置信限。然后使用指数函数将这些估计值和它们的置信限转换回原始单位。
使用 Fisher 信息矩阵估计参数的协方差矩阵(请参见Crow-AMSAA 模型的参数估计值)。但是,在生成的公式中用 MLE 替换 λ 和 β 的修正偏倚的估计值。图中的所有置信带和报表中的置信区间均基于该过程。
对于 Crow-AMSAA 模型,通过用来自 MLE 的参数替换理论表达式中的参数 λ 和 β,得到刻画器中给出的 MTBF、强度和累积事件的估计值。选择“使用修改 MLE 的 Crow-AMSAA”选项时,使用修改的 MLE。通过将 delta 方法应用到相关表达式的对数,得到置信限。
例如,考虑累积事件函数。自检验开始以来在时间 t 处的累积事件数由 N(t) = λtβ 给出。它满足 log(N(t)) = log(λ) + βlog(t)。用 MLE(或修改的 MLE)替换 log(N(t)) 中的参数 λ 和 β 来估计 log(N(t))。将 delta 方法应用到该表达式来获得其方差的估计值。该估计值用于构造基于 Wald 的 95% 置信区间。然后使用指数函数转换所得的置信限以给出在 t 时间处估计的累积事件数的置信限。
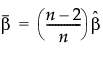 用于定数截尾的检验
用于定数截尾的检验 用于定时截尾的检验
用于定时截尾的检验