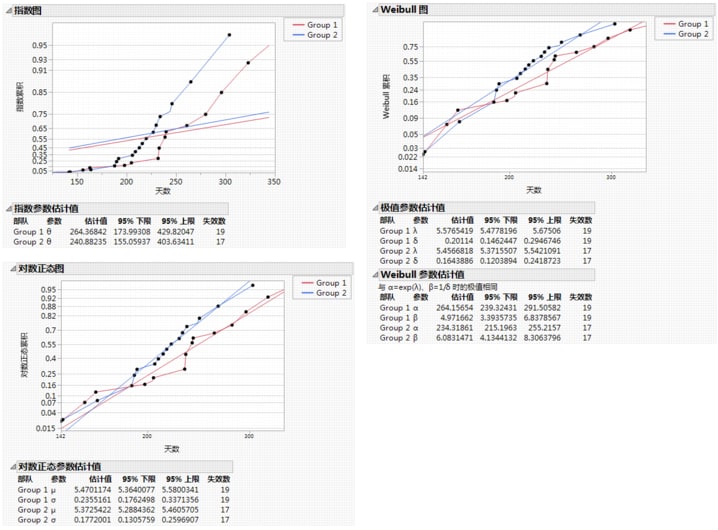
Weibull 分布对于事件时间数据是最常见的。不同作者有很多方式来参数化该分布(如依照 JMP 的 alpha 和 beta 的各种 Weibull 参数中所示)。JMP 报告了两个参数化方式,标记为 lambda-delta 极值参数化和 Weibull alpha-beta 参数化。在可靠性文献中使用 alpha-beta 参数化。请参见 Nelson (1990)。将 Alpha 解释为 63.2% 的单元失效时的分位数。按以下方式解释 Beta:若 beta>1,则危险率随时间增加;若 beta<1,则危险率随时间下降;若 beta=1,则危险率为常数,这表示它是指数分布。
|
alpha=alpha
|
beta=beta
|
|
|
eta=alpha
|
beta=beta
|
|
|
c = alpha
|
m = beta
|
|
|
eta=alpha
|
beta=beta
|
|
|
exp(X beta)=alpha
|
lambda=beta
|
|
|
beta=alpha
|
alpha=beta
|
|
|
lambda = 1/alpha
|
p = beta
|
|
|
lambda=log(alpha)
|
delta=1/beta
|
|
|
mu=log(alpha)
|
sigma=1/beta
|
要查看指数、Weibull 和对数正态拟合的其他选项,请按住 Shift 键,点击乘积限生存拟合菜单的红色小三角菜单,然后点击所需的拟合。
在拟合相应分布时,JMP 可以约束 Theta(指数)、Beta (Weibull) 和 Sigma(对数正态)参数的值。在 WeiBayes 情形中需要该功能,例如: