Multicollinearity
What is multicollinearity?
The term multicollinearity refers to the condition in which two or more predictors in a regression model are highly correlated with one another and exhibit a strong linear relationhip.
See how to assess multicollinearity using statistical software
Excerpt from Statistical Thinking for Industrial Problem Solving, a free online statistics course
- Learn more by enrolling in the Correlation and Regression module of our free statistics course.
- Download a free trial of JMP to try it yourself.
Why is multicollinearity a problem?
In a regression context, multicollinearity can make it difficult to determine the effect of each predictor on the response, and can make it challenging to determine which variables to include in the model. Multicollinearity can also cause other problems:
- The coefficients might be poorly estimated, or inflated.
- The coefficients might have signs that don’t make sense.
- The standard errors for these coefficients might be inflated.
Multicollinearity example
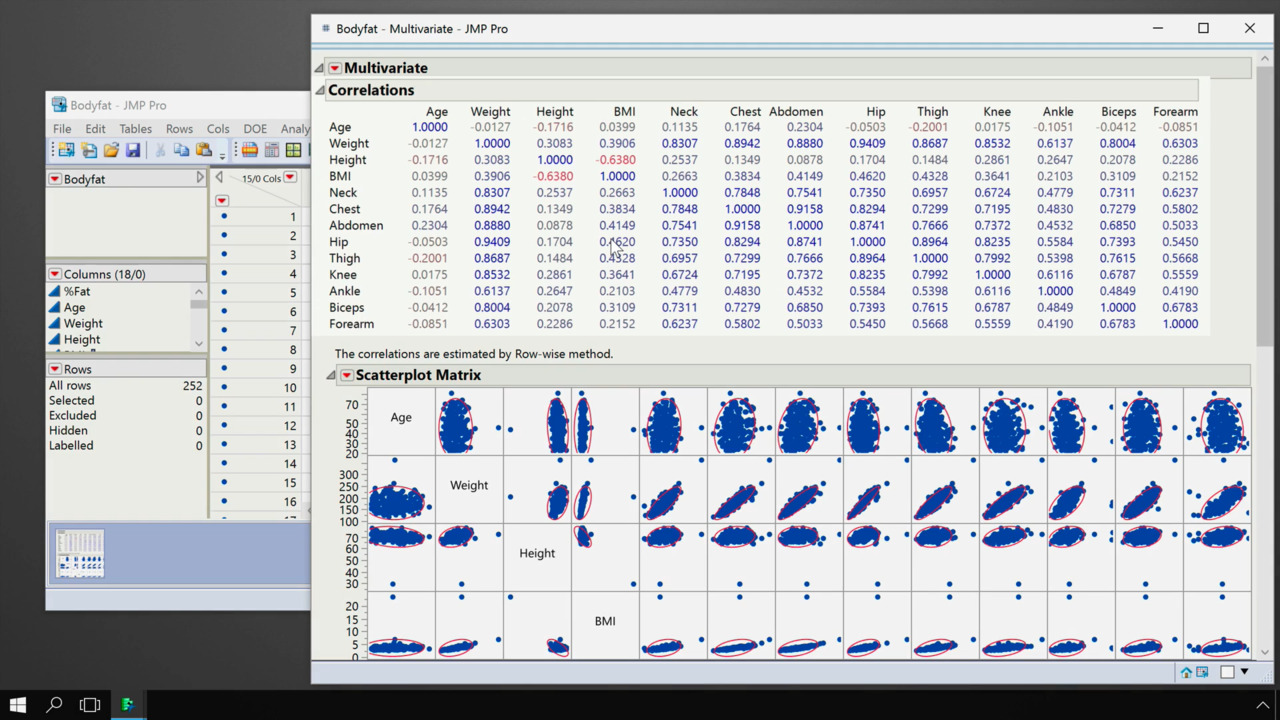
For illustration, we take a look at a new example, Bodyfat. This data set includes measurements of 252 men. The goal of the study was to develop a model, based on physical measurements, to predict percent body fat. We focus on a subset of the potential predictors: Weight (in pounds), Height (in inches), and BMI (Body Mass Index).
Weight is highly correlated with BMI, and is moderately correlated with Height.
We fit a model to predict Fat% as a function of these three variables. BMI and Weight are significant, and Height is borderline significant.
But BMI is a function of both Weight and Height. So, there is some redundant information in these predictors.
What happens if we remove BMI from the model?
Notice how the parameter estimates for Weight and Height have changed.
- The coefficient for Weight changed from negative to positive.
- The coefficient for Height changed from positive to negative.
Both Weight and Height are also now highly significant. Another dramatic change is in the accuracy of the estimates. The standard errors for Weight and Height are much larger in the model containing BMI.
Detecting multicollinearity with the variance inflation factor (VIF)
When we fit a model, how do we know if we have a problem with multicollinearity? As we've seen, a scatterplot matrix can point to pairs of variables that are correlated. But multicollinearity can also occur between many variables, and this might not be apparent in bivariate scatterplots.
One method for detecting whether multicollinearity is a problem is to compute the variance inflation factor, or VIF. This is a measure of how much the standard error of the estimate of the coefficient is inflated due to multicollinearity. The VIF for a predictor is calculated using this formula.
For a given predictor variable, a regression model is fit using that variable as the response and all the other variables as predictors. The RSquare for this model is calculated, and the VIF is computed. This is repeated for all predictors. The smallest possible value of VIF is 1.0, indicating a complete absence of multicollinearity. Statisticians use the term orthogonal to refer to variables that are completely uncorrelated with one another.
A VIF for a predictor of 10.0 corresponds to an RSquare value of 0.90. Likewise, a VIF of 100 corresponds to an RSquare of 0.99. This would mean that the other predictors explain 99% of the variation in the given predictor. In most cases, there will be some amount of multicollinearity. As a rule of thumb, a VIF of 5 or 10 indicates that the multicollinearity might be problematic. In our example, the VIFs are all very high, indicating that multicollinearity is indeed an issue.
After we remove BMI from the model, the VIFs are now very low.
In some cases, multicollinearity can be resolved by removing a redundant term from the model. In more severe cases, simply removing a term will not address the issue. In these cases, more advanced techniques such as principal component analysis (PCA) or partial least squares (PLS) might be appropriate. Other modeling approaches, such as tree-based methods and penalized regression, are also recommended.