|
1.
|
|
2.
|
Select Analyze > Fit Model.
|
|
3.
|
|
4.
|
|
5.
|
|
6.
|
Click Run.
|
The model fit in this example reduces the –LogLikelihood of 429.9 for the intercept-only model to 355.67 for the full model. This reduction yields a likelihood ratio chi-square statistic for the whole model of 148.45 with 3 degrees of freedom. Therefore, the difference in perceived cheese taste is highly significant.
The most preferred cheese additive is the one with the most negative parameter estimate. Cheese[D] does not appear in the Parameter Estimates report, because it does not have its own column of the design matrix. However, Cheese D’s effect can be computed as the negative sum of the others, and is shown in Preferences for Cheese Additives in Cheese.jmp.
As an ordinal problem, each of the first eight response levels has an intercept, but there are only three parameters for the four levels of Cheese. As a result, there are 3 degrees of freedom in the ordinal model. The ordinal model is the Fitted model in the Lack of Fit test.
There are 28 rows with a nonzero value of Count in the data table, so there are 28 - 4 = 24 replicated points with respect to the levels of Cheese. Therefore, the Saturated model in the Lack of Fit test has 24 degrees of freedom.
As a nominal problem, each of the first eight response levels has an intercept as well as three parameters for the four levels of Cheese. As a result, there are 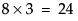 degrees of freedom in the nominal model. Therefore, the nominal model is the Saturated model in the Lack of Fit test.
degrees of freedom in the nominal model. Therefore, the nominal model is the Saturated model in the Lack of Fit test.
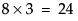 degrees of freedom in the nominal model. Therefore, the nominal model is the Saturated model in the Lack of Fit test.
degrees of freedom in the nominal model. Therefore, the nominal model is the Saturated model in the Lack of Fit test.