statistics, and computes sigma as follows:
Note: By default, the capability indices in the Long Term Sigma report use the Cp labeling that is used in the other sigma reports. To use Ppk labeling in the Long Term Sigma report, select the File > Preferences > Platforms > Distribution > PpK Capability Labeling preference.
is the average of the moving ranges.d2(n) is the expected value of the range of n independent normally distributed variables with unit standard deviation.
If r is the number of subgroups of size nj and each ith subgroup is defined by the order of the data, sigma is computed as follows:
where 
(Appears only for capability analyses based on fitted distributions.) Uses the square root of the variance of the fitted distribution. For more information about the relationship between the parameters in the Parameter Estimates report and the expected value and variance of the fitted distributions, see Continuous Fit Distributions and Discrete Fit Distributions.
For a process characteristic with mean μ and standard deviation σ, the population-based capability indices are defined as follows.
LSL is the lower specification limit.
USL is the upper specification limit.
T is the target value.
For sample-based capability indices, the parameters are replaced by their estimates. The estimate for σ uses the method that you specified in the Capability Analysis window. See Variation Statistics.
The 100(1 - α)% confidence interval for Cp is calculated as follows:
is the estimated value for Cp.
is the (n is the number of observations.
The 100(1 - α)% confidence interval for Cpk is calculated as follows:
is the estimated value for Cpk.
is the (1 - n is the number of observations.
The 100(1 - α)% confidence interval for CPM is calculated as follows:
is the estimated value for CPM.
is the (
n is the number of observations.
is the mean of the observations.T is the target value.
s is the long-term sigma estimate.
Lower and upper confidence limits for CPL and CPU are computed using the method of Chou et al. (1990).
The 100(1 - α)% confidence limits for CPL (denoted by CPLL and CPLU) satisfy the following equations:
where 
where 
tn-1(δ) has a non-central t-distribution with n - 1 degrees of freedom and noncentrality parameter δ.
is the estimated value for Cpl.The 100(1 - α)% confidence limits for CPU (denoted by CPUL and CPUU) satisfy the following equations:
where 
where 
tn-1(δ) has a non-central t-distribution with n - 1 degrees of freedom and noncentrality parameter δ.
is the estimated value for Cpu.
LSL is the lower specification limit.
USL is the upper specification limit.
T is the target value.
For the calculation of Cpm, μ and σ are estimated using the expected value and square root of the variance of the fitted distribution. For more information about the relationship between the parameters in the Parameter Estimates report and the expected value and variance of the fitted distributions, see Continuous Fit Distributions and Discrete Fit Distributions.
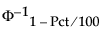is the (1 - Pct/100)th quantile of a standard normal distribution.
= 3 * Cpl
= 3 * CpuLSL is the lower specification limit.
USL is the upper specification limit.
μ is the sample mean.
σ is the sample standard deviation.
is the (1 - Φ is the standard normal cumulative distribution function.