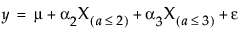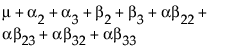noting that μ is the expected response at A = 1, μ + α2 is the expected response at A = 2, and μ + α2 + α3 is the expected response at A = 3. Thus, α2 estimates the effect moving from A = 1 to A = 2 and α3 estimates the effect moving from A = 2 to A = 3.
To see what the parameters mean, examine this table of the expected cell means in terms of the parameters, where μ is the intercept, α2 is the parameter for level A2, and so on.
Note that the main effect test for A is really testing the A levels holding B at the first level. Similarly, the main effect test for B is testing across the top row for the various levels of B holding A at the first level. This is the appropriate test for an experiment where the two factors are both doses of different treatments. The main question is the efficacy of each treatment by itself, and fewer points are devoted to looking for drug interactions when doses of both drugs are applied. In some cases, it might even be dangerous to apply large doses of each drug.
The example is the same as above, with two observations per cell except that the A3B2 cell has no data. You can now compare the results when the factors are coded nominally with results when they are coded ordinally. The model fit is the same, as seen in Figure 12.2.
The effect tests lose degrees of freedom for nominal. In the case of B, there is no test. For ordinal, there is no loss because there is no missing cell for the base first level.
The least squares means are also different. The nominal LSMs are not all estimable, but the ordinal LSMs are. You can verify the values by looking at the cell means. Note that the A*B LSMs are the same for the two. Figure 12.6 shows least squares means for nominal and ordinal fits.