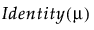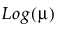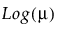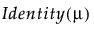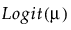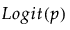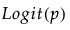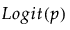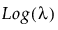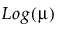Distribution

When you select Generalized Regression from the Personality menu, the Distribution option appears. Here you can specify a distribution for Y. The abbreviation ZI means zero-inflated. The distributions are separated into three categories based on their response: continuous, discrete, and zero-inflated. The options are described below.

Note: If you specify multiple Y variables in the Model Specification window, the same response distribution must be used for all of the specified Y variables. If you want to fit separate distributions to different response variables in the same Generalized Regression report, you must use a script.

Continuous

Normal

Y has a normal distribution with mean μ and standard deviation σ. The normal distribution is symmetric and with a large enough sample size, can approximate a large variety of other distributions using the Central Limit Theorem. The link function for μ is the identity. That is, the mean of Y is expressed as a linear model.

Note: When the specified Distribution is Normal, Standard Least Squares replaces the Maximum Likelihood Estimation method.

The scale parameter for the normal distribution is σ. When there is no penalty in the estimation method, the estimate of the scale parameter σ is the root mean square error (RMSE). The RMSE is the square root of the usual unbiased estimator of σ2. The results shown are equivalent to a standard least squares fit unless censored observations are involved.

Note: The parameterization of nominal variables used in the Generalized Regression personality differs from their parameterization using the Standard Least Squares personality. Because of this difference, parameter estimates differ for models that contain nominal or ordinal effects.

See Statistical Details for Distributions.

Cauchy

Y has a Cauchy distribution with location parameter μ and scale parameter σ. The Cauchy distribution has an undefined mean and standard deviation. The median and mode are both μ. Most data do not inherently follow a Cauchy distribution. However, it is useful for conducting a robust regression on data that contain a large proportion of outliers (up to 50%). The link function for μ is the identity. See Statistical Details for Distributions.

Exponential

Y has an exponential distribution with mean parameter μ. The exponential distribution is right-skewed and is often used to model lifetimes or the time between successive events. The link function for μ is the logarithm. See Statistical Details for Distributions.

Gamma

Y has a gamma distribution with mean parameter μ and dispersion parameter σ. The gamma is a flexible distribution and contains a family of other widely used distributions. For example, the exponential distribution is a special case of the gamma distribution where σ = μ. The chi squared distribution can also be derived from the gamma distribution. The link function for μ is the logarithm. See Statistical Details for Distributions.

Weibull

Y has a Weibull distribution with mean parameter μ and scale parameter σ. The Weibull distribution is flexible and is often used to model lifetimes or the time until an event. The link function for μ is the identity. See Statistical Details for Distributions.

LogNormal

Y has a Lognormal distribution with mean parameter μ and scale parameter σ. The Lognormal distribution is right-skewed and is often used to model lifetimes or the time until an event. The link function for μ is the identity. See Statistical Details for Distributions.

Beta

Y has a beta distribution with mean parameter μ and dispersion parameter σ. The response for the beta is between 0 and 1 (not inclusive) and is often used to model proportions or rates. The link function for μ is the logit. See Statistical Details for Distributions.

Quantile Regression

Quantile regression models a specified conditional quantile of the response. No assumption is made about the form of the underlying distribution. When you select Quantile Regression, a Quantile box appears beneath the Distribution menu. Specify the desired quantile.

If you specify 0.5 (the default) for the Quantile on the Model Dialog window, quantile regression models the conditional median of the response. Quantile regression is particularly useful when the rate of change in the conditional quantile, expressed by the regression coefficients, depends on the quantile. An advantage of quantile regression over least squares regression is its flexibility for modeling data with heterogeneous conditional distributions.

Quantile Regression is fit by minimizing an objective function using an iterative approach. For more information about quantile regression, see Koenker and Hallock (2001) and Portnoy and Koenker (1997).

When you choose Quantile Regression, Maximum Likelihood is the only available Estimation Method, and None is the only available Validation Method.

Note: If a quantile regression fit is time intensive, a progress bar appears. The progress bar shows the relative change in the objective function. When you click Accept Current Estimates, the calculation stops and the reported parameter estimates correspond to the best model fit at that point.

Cox Proportional Hazards

The Cox proportional hazards model is a regression model for time-to-event data with predictors. It is based on a multiplicative relationship between the predictors and the hazard function. It can be used to examine the effect of predictors on survival times. The model involves an arbitrary baseline hazard function that is scaled by the predictors to give a general hazard function. The proportional hazards model produces parameter estimates and standard errors for each predictor. The Cox proportional hazards model was first proposed by D. R. Cox (1972). For more information about proportional hazards models, see Kalbfleisch and Prentice (2002).

When you choose Cox Proportional Hazards, the only available Validation Methods are BIC and AICc. Also, the Ridge Estimation Method is not available.

Note: When there are ties in the response, the Efron likelihood is used. See Efron (1977). This is a different method for handling ties than is used in the Proportional Hazard personality of the Fit Model platform or in the Fit Proportional Hazards platform.

Discrete

Binomial

Y has a binomial distribution with parameters p and n. The response, Y, indicates the total number of successes in n independent trials with a fixed probability, p, for all trials. This distribution allows for the use of a sample size column. If no column is listed, it is assumed that the sample size is one. The link function for p is the logit. When you select a binary response variable that has a Nominal modeling type, Binomial is the only available response distribution. See Statistical Details for Distributions.

When you select Binomial as the Distribution, the response variable must be specified in one of the following ways.

–

Unsummarized: If your data are not summarized as frequencies of events, specify a single binary column as the response. If this column has a modeling type of Nominal, you can designate one of the levels to be the Target Level.

–

Summarized with Freq column: If your data are summarized as frequencies of successes and failures, specify a single binary column as the response. If this column has a modeling type of Nominal, you can designate one of the levels to be the Target Level. Assign the frequency column to the Freq role.

–

Summarized with sample size column entered as second Y: If your data are summarized as frequencies of events (successes) and trials, specify two continuous columns as Y in this order: the count of the number of successes, and the count of the number of trials.

Note: When the specified Distribution is Binomial, Logistic Regression replaces the Maximum Likelihood Estimation method.

Beta Binomial

Y has a beta binomial distribution with the probability of success, p, the number of trails, n, and overdispersion parameter, δ. This distribution is an overdispersed version of the binomial distribution.

Run demoBetaBinomial.jsl in the JMP Samples/Scripts folder to compare a beta binomial distribution with dispersion parameter δ to a binomial distribution with parameters p and n = 20.

The beta binomial distribution requires a sample size greater than one for each observation. Thus, the user must specify a sample size column. To insert a sample size column, specify two continuous columns as Y in this order: the count of the number of successes, and the count of the number of trials. The link function for p is the logit. See Statistical Details for Distributions.

Multinomial

Y has a multinomial distribution with three or more discrete levels. The response variable must have a nominal or ordinal modeling type. The model fits separate intercepts and effects parameters for each level of the response variable. If the response variable has k levels, the model contains k - 1 intercepts and effects parameters. The link function for the Multinomial distribution is the multinomial logit. See Nominal Responses in Statistical Details.

Ordinal Logistic

Y has a multinomial distribution with ordinal levels. The response variable must have an ordinal modeling type. The model fits an intercept for each level of the response variable. The effects parameters are common across all levels of the response variable. The link function for the Ordinal Logistic distribution is the ordered logit. See Ordinal Responses in Statistical Details.

Note: The intercept parameterization for Ordinal Logistic in Generalized Regression differs from that in the Ordinal Logistic personality of Fit Model. The first Intercept term in Generalized Regression corresponds to the first Intercept term in the Ordinal Logistic personality. The subsequent Intercept terms in Generalized Regression are the successive differences between the intercept terms for the ordered levels of the response variable.

Poisson

Y has a Poisson distribution with mean λ. The Poisson distribution typically models the number of events in a given interval and is often expressed as count data. The link function for λ is the logarithm. Poisson regression is permitted even if Y assumes non-integer values. See Statistical Details for Distributions.

Negative Binomial

Y has a negative binomial distribution with mean μ and dispersion parameter σ. The negative binomial distribution typically models the number of successes before a specified number of failures. The negative binomial distribution is also equivalent to the Gamma Poisson distribution under certain conditions. For more details about the connection between negative binomial and Gamma Poisson, see Distributions in the Basic Analysis book.

Run demoGammaPoisson.jsl in the JMP Samples/Scripts folder to compare a Gamma Poisson distribution with mean λ and dispersion parameter σ to a Poisson distribution with mean λ.

The link function for μ is the logarithm. Negative binomial regression is permitted even if Y assumes non-integer values. See Statistical Details for Distributions.

Zero-Inflated

ZI Binomial

Y has a zero-inflated binomial distribution with parameters p, n, and zero-inflation parameter π. The response, Y, indicates the total number of successes in n independent trials with a fixed probability, p, for all trials. This distribution allows for the use of a sample size column. If no column is listed, it is assumed that the sample size is one. The link function for p is the logit. See Statistical Details for Distributions.

ZI Beta Binomial

Y has a beta binomial distribution with the probability of success, p, the number of trails, n, overdispersion parameter, δ, and zero-inflation parameter π. This distribution is an overdispersed version of the ZI binomial distribution. The ZI beta binomial distribution requires a sample size greater than one for each observation. Thus, the user must specify a sample size column. To insert a sample size column, specify two continuous columns as Y in this order: the count of the number of successes, and the count of the number of trials. The link function for p is the logit. See Statistical Details for Distributions.

ZI Poisson

Y has a zero-inflated Poisson distribution with mean parameter λ and zero-inflation parameter π. The parameter λ is the conditional mean based on the observations coming from the Poisson distribution and not the inflating zeros. The link function for λ is the logarithm. ZI Poisson regression is permitted even if Y assumes no observed zeros or non-integer values. See Statistical Details for Distributions.

ZI Negative Binomial

Y has a zero-inflated negative binomial with location parameter μ, dispersion parameter σ, and zero-inflation parameter π. The parameter μ is the conditional mean based on the observations coming from the negative binomial distribution and not the inflating zeros. The link function for μ is the logarithm. ZI negative binomial regression is permitted even if Y assumes no observed zeros or non-integer values. See Statistical Details for Distributions.

ZI Gamma

Y has a zero-inflated gamma distribution with mean parameter μ and zero-inflation parameter π. Many times, we might believe that our nonzero responses are gamma distributed. This is true for insurance claims: claim values are approximately gamma distributed but there are also zeros in the data for policies that do not have any claims. The zero-inflated gamma could handle such data directly without having to split the data into zero and nonzero responses. The parameter μ is the conditional mean based on observations coming from the gamma distribution and not the inflating zeros. The link function for μ is the logarithm. See Statistical Details for Distributions.

Table 6.1 gives the Data Types, Modeling Types, and other requirements for Y variables assigned the various distributions.

Table 6.1 Requirements for Y for Distributions
Distribution	Data Type	Modeling Type	Other
Normal	Numeric	Continuous
Cauchy	Numeric	Continuous
Exponential	Numeric	Continuous	Positive
Gamma	Numeric	Continuous	Positive
Weibull	Numeric	Continuous	Positive
LogNormal	Numeric	Continuous	Positive
Beta	Numeric	Continuous	Between 0 and 1
Quantile Regression	Numeric	Continuous
Cox Proportional Hazards	Numeric	Continuous	Nonnegative
Binomial, unsummarized	Any	Any	Binary
Binomial, summarized with Freq column	Any	Any	Binary
Binomial, summarized with count column entered as second Y	Numeric	Continuous	Nonnegative
Beta Binomial	Numeric	Continuous	Nonnegative
Multinomial	Any	Ordinal or Nominal
Ordinal Logistic	Any	Ordinal
Poisson	Numeric	Any	Nonnegative
Negative Binomial	Numeric	Any	Nonnegative
Zero-Inflated Binomial	Numeric	Any	Nonnegative
Zero-Inflated Beta Binomial	Numeric	Any	Nonnegative
Zero-Inflated Poisson	Numeric	Any	Nonnegative
Zero-Inflated Negative Binomial	Numeric	Any	Nonnegative
Zero-Inflated Gamma	Numeric	Continuous	Nonnegative

For more information about how these distributions are parameterized, see Statistical Details for Distributions. Table 6.2 summarizes the details.

Table 6.2 Distributions, Parameters, and Link Functions
Distribution	Parameters	Mean Model Link Function
Normal	μ, σ
Cauchy	μ, σ
Exponential	μ
Gamma	μ, σ
Weibull	μ, σ
LogNormal	μ, σ
Beta	μ
Binomial	n, p
Beta Binomial	n, p, δ
Poisson	λ
Negative Binomial	μ, σ
Zero-Inflated Binomial	n, p, π (zero-inflation)
Zero-Inflated Beta Binomial	n, p, δ, π (zero-inflation)
Zero-Inflated Poisson	λ, π (zero-inflation)
Zero-Inflated Negative Binomial	μ, σ, π (zero-inflation)
Zero-Inflated Gamma	μ, σ, π (zero-inflation)

After selecting an appropriate Distribution, click Run. The Generalized Regression report window appears.