Example of Interval Censoring
In this example, use the Survival platform to implement the Turnbull method, which is used to obtain nonparametric estimates of the survival function. With interval-censored data, you know only that the events occurred in some time interval.
In this example, microprocessor units are tested and inspected at various times and the failed units are counted. Missing values in one of the columns indicate that you do not know the lower or upper limit, and therefore the event is left or right censored, respectively.
1. Select Help > Sample Data Folder and open Reliability/Microprocessor Data.jmp.
2. Select Analyze > Reliability and Survival > Survival.
3. Select start time and end time and click Y, Time to Event.
4. Select count and click Freq.
5. Select the check box next to Plot Failure instead of Survival.
6. Click OK.
7. Click the red triangle next to Product-Limit Survival Fit and select LogNormal Fit.
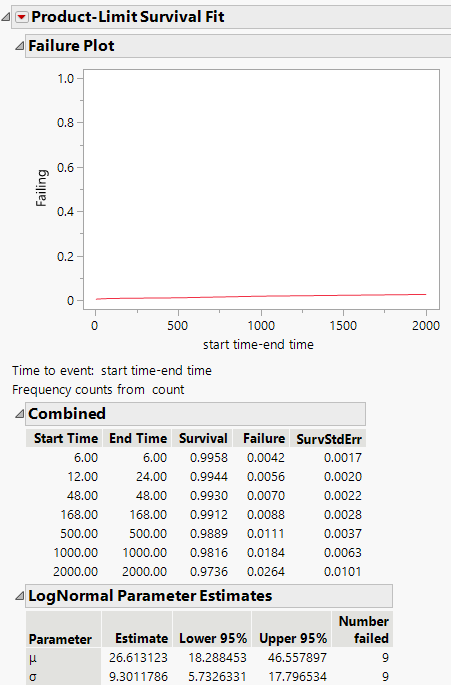
Figure 14.14 Interval Censoring Output
The resulting Turnbull estimates are shown. Turnbull estimates might have gaps in time where the survival probability is not estimable. In this example, such gaps occur between 6 and 12, 24 and 48, 48 and 168, and so on.
At this point, select a distribution to see its fitted estimates —in this case, a Lognormal distribution is fit. Notice that the failure plot shows very small failure rates for these data.