 Statistical Details for Saved Probability Formulas
Statistical Details for Saved Probability Formulas
This section describes the formulas saved using the Save Probability Formula option in the Naive Bayes red triangle menu. The conditional probability that an observation with predictor values x1, x2, …, xp belongs in the class Ck differs slightly from that given by P(Ck|(x1,..., xp)), shown in the section Statistical Details for the Naive Bayes Algorithm. This is done for computational efficiency.
Naive Score Formulas
The Naive Score formula for a given class Ck, S(Ck), is a variation of the numerator in the expression for P(Ck|(x1,..., xp)) and is computed as follows:
S(Ck) = exp[ln{P(Ck)} + Continuous + Categorical + ln(R)]
The Naive Score formula is a combination of scores from continuous and categorical predictors. Recall that R is a regularization constant. The continuous portion of the formula is computed as follows:
Continuous = 
where
j = 1,..., p1 continuous predictors.
The categorical portion of the formula is computed as follows:
Categorical = 
where
r= 1,...,p2 categorical variables
l = 1,..., Lr levels of the rth categorical variable
1rl is an indicator variable that equals 1 when xrl is the lth level of the rth categorical predictor and 0 otherwise
Naive Score Sum Formulas
The Naive Score Sum formula, S, sums the Naive Score formulas over all classes. This is a variation of the denominator in the expression for P(Ck|(x1,..., xp)).
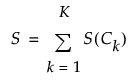
Naive Prob Formulas
The Naive Prob formula for a given class Ck equals P(Ck|(x1,..., xp)). In the JMP formulas,
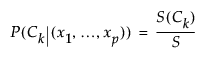
Naive Predicted Formula
The Naive Predicted Formula for an observation classifies that observation into the class for which P(Ck|(x1,..., xp)) is the largest. This is equivalent to classifying an observation into the class for which its Naive Score formula is the largest.