Statistical Details for Tests That the Variances Are Equal
This section contains details for the Tests That the Variances Are Equal report in the Oneway platform.
F Ratio
O’Brien’s test constructs a dependent variable so that the group means of the new variable equal the group sample variances of the original response. The O’Brien variable is computed as follows:
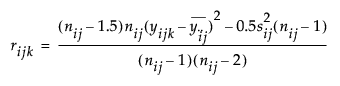
where n represents the number of yijk observations.
Brown-Forsythe is the model F statistic from an ANOVA on 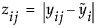 where
where 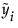 is the median response for the ith level.
is the median response for the ith level.
The Levene F is the model F statistic from an ANOVA on 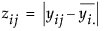 where
where 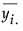 is the mean response for the ith level.
is the mean response for the ith level.
Bartlett’s test is calculated as follows:
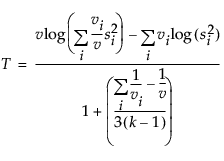 where
where 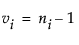 and
and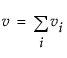
and ni is the count on the ith level and si2 is the response sample variance on the ith level. The Bartlett statistic has a χ2-distribution. Dividing the Chi-square test statistic by the degrees of freedom results in the reported F value.
Welch’s Test F Ratio
The Welch’s Test F Ratio is computed as follows:
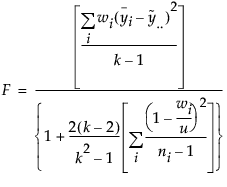 where
where 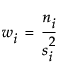 ,
, 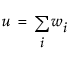 ,
, 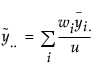 ,
,
and ni is the count on the ith level, 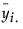 is the mean response for the ith level, and si2 is the response sample variance for the ith level.
is the mean response for the ith level, and si2 is the response sample variance for the ith level.
Welch’s Test DF Den
The Welch approximation for the denominator degrees of freedom is defined as follows:
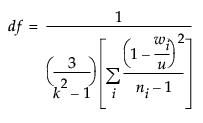
where wi, ni, and u are defined as in the F ratio formula.