For the latest version of JMP Help, visit JMP.com/help.


Multivariate Methods > Multidimensional Scaling > Statistical Details for the Multidimensional Scaling Platform > Statistical Details for the Stress Function
Publication date: 05/05/2023

Statistical Details for the Stress Function

In the Multidimensional Scaling platform, a quasi-Newton optimization method is used to minimize the Stress function to determine the MDS coordinates. This minimization leads to a set of coordinates in a predetermined number of dimensions that minimize the derived proximity measures for each pairwise set of the dimensions. When the data are ordinal, monotonic regression is used. Otherwise, standard least squares regression is used.

The following notation is used to define Stress:

• i, j - indexes for the number of objects

• dij - the derived distance between objects i and j

δij - the observed relative distance between objects i and j

• f(δrs) - transformation function for the distance

The Stress function is defined as follows:

Stress = 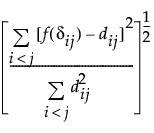Equation shown here

This measure of stress is also known as Kruskal’s Stress, Type I, or simply Stress1.

Want more information? Have questions? Get answers in the JMP User Community (community.jmp.com).