Statistical Details for the van der Voet T2 Test
In the Partial Least Squares platform, the van der Voet T2 test helps determine whether a model with a specified number of extracted factors differs significantly from a proposed optimum model. The test is a randomization test based on the null hypothesis that the squared residuals for both models have the same distribution. Intuitively, one can think of the null hypothesis as stating that both models have the same predictive ability.
To obtain the van der Voet T2 statistic given in the Cross Validation report, the calculation below is performed on each validation set. In the case of a single validation set, the result is the reported value. In the case of Leave-One-Out and KFold validation, the results for each validation set are averaged.
Denote by Ri, jk the jth predicted residual for response k for the model with i extracted factors. Denote by Ropt, jk is the corresponding quantity for the model based on the proposed optimum number of factors, opt. The test statistic is based on the following differences:
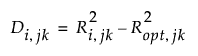
Suppose that there are K responses. Consider the following notation:
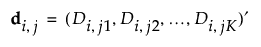
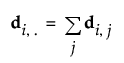

The van der Voet statistic for i extracted factors is defined as follows:
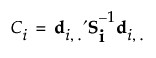
The significance level is obtained by comparing Ci with the distribution of values that results from randomly exchanging R2i,jk and R2opt,jk. A Monte Carlo sample of such values is simulated and the significance level is approximated as the proportion of simulated critical values that are greater than or equal to Ci.