Example of Mixture Variables with a Process Variable
This example uses the prediction formula from a response surface model to create a Mixture Profiler. You set a feasible region that achieves a certain response and explore the different combinations of factor values that are within the feasible region.
The data comes from an experiment to optimize the texture of fish patties. There are three mixture components that each represent the proportion of a fish type in the fish patty. There is also a process variable that is the oven temperature used to bake the patties. The response is a measure of texture acceptability, where higher is better.
1. Select Help > Sample Data Folder and open Fish Patty.jmp.
2. Select Graph > Mixture Profiler.
3. Select Predicted Rating and click Y, Prediction Formula.
4. Click OK.
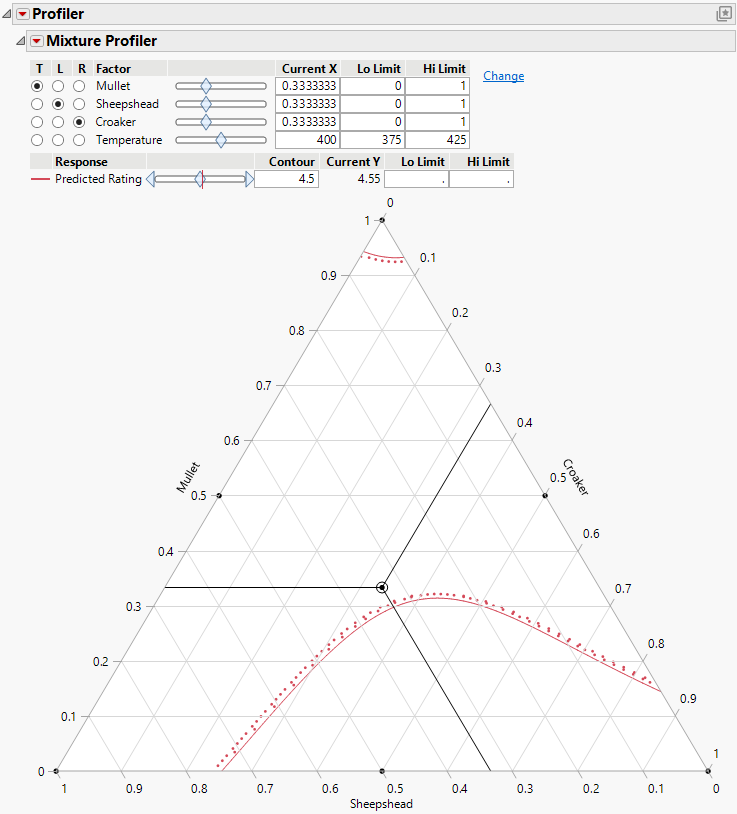
Figure 6.8 Initial Output for Mixture Profiler
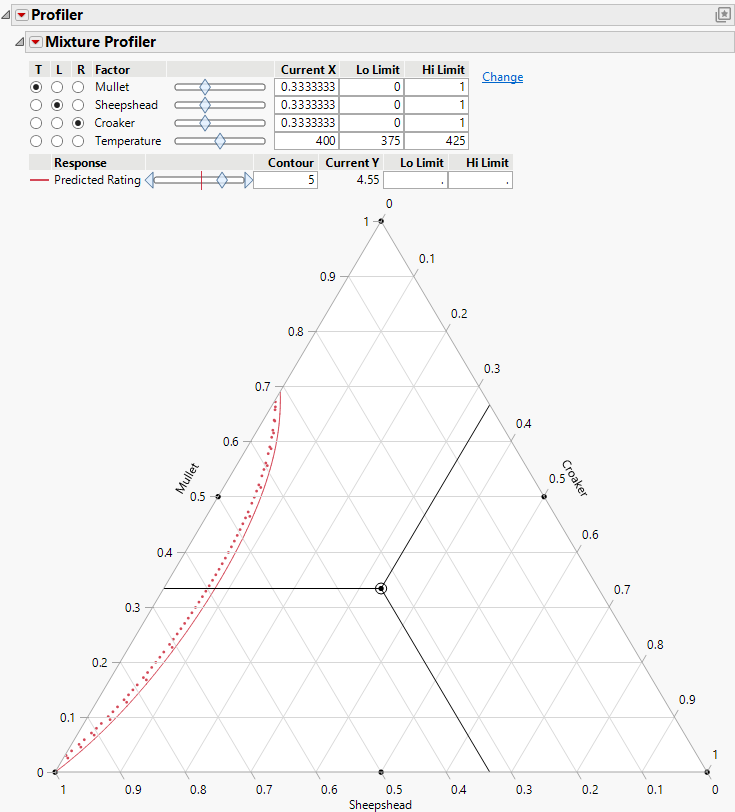
5. The manufacturer wants the rating to be at least 5. Use the slider control for Predicted Rating to move the contour close to 5. Alternatively, you can enter 5 in the Contour edit box to set the contour to 5.
Figure 6.9 Contour Showing a Predicted Rating of 5
The Up Dots shown along the contour indicate the direction of increasing Predicted Rating.
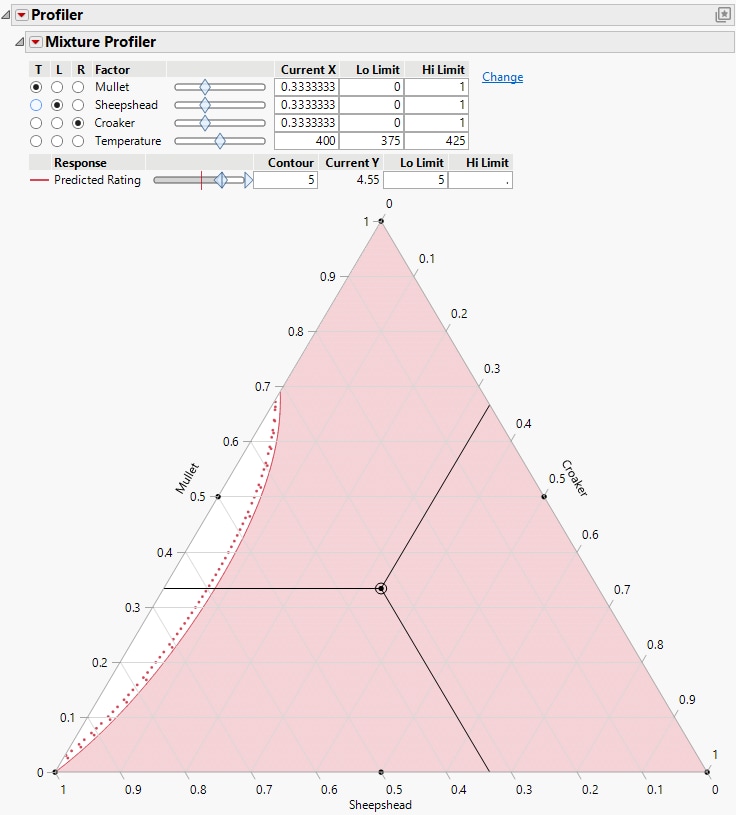
6. Enter 5 in the Lo Limit edit box for the Predicted Rating. The resulting shaded region represents factor combinations that yield a rating less than 5. To produce patties with at least a rating of 5, the manufacturer can set the factors values anywhere in the feasible (unshaded) region. The region has small proportions of Croaker (<10%), mid to low proportions of Mullet (<70%) and mid to high proportions of Sheepshead (>30%). This region is for a baking temperature of 400 degrees.
Figure 6.10 Contour Shading Showing Predicted Rating of 5 or More.
7. Move the slide control for Temperature to observe how the feasible region changes for different temperature settings.
Additional analyses might include:
• Optimize the response across all four factors simultaneously. See “Custom Profiler” or “Desirability Profiling and Optimization”.
• Simulate the response as a function of the random variation in the factors and model noise. See “Simulator”.