Example of the Nonparametric Wilcoxon Test
In the Oneway platform, use a Wilcoxon test to determine whether the mean profit earned by companies differs by type of company. The data consist of various metrics on two types of companies, Pharmaceutical (12 companies) and Computer (20 companies).
1. Select Help > Sample Data Folder and open Companies.jmp.
2. Select Analyze > Fit Y by X.
3. Select Profits ($M) and click Y, Response.
4. Select Type and click X, Factor.
5. Click OK.
6. Click the Oneway Analysis red triangle and select Display Options > Box Plots.
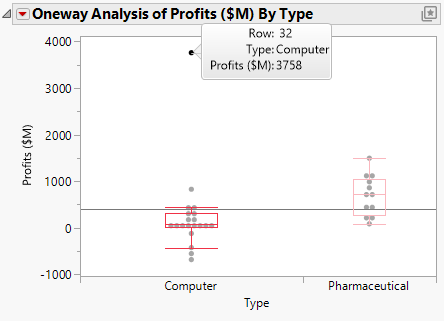
Figure 6.22 Computer Company Profit Distribution
The box plots suggest that the distributions of profits within groups are not normal or symmetric. There is a very large value for the company in row 32 that might affect parametric tests.
7. Click the Oneway Analysis red triangle menu and select Nonparametric > Wilcoxon / Kruskal-Wallis Test.
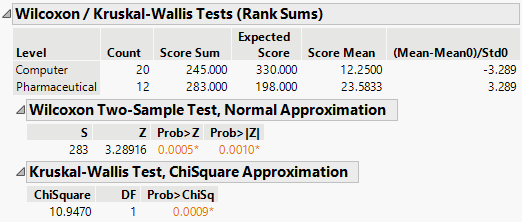
Figure 6.23 Wilcoxon Test Results
Both the normal approximation that uses a 0.5 continuity correction and the chi-square approximation for the Wilcoxon test statistic indicate significance at a p-value less than or equal to 0.0010. You conclude that there is a significant difference in the location of the distributions, and conclude that mean profit differs based on company type.
The normal and chi-square tests are based on the asymptotic distributions of the test statistics. You can also conduct an exact test.
8. Click the Oneway Analysis red triangle menu and select Nonparametric > Exact Test > Wilcoxon Exact Test.
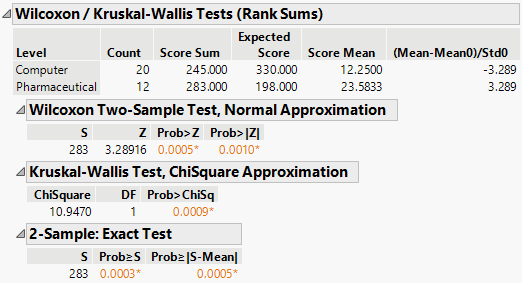
Figure 6.24 Wilcoxon Exact Test Results
The observed value of the test statistic is S = 283. This is the sum of the ranks for the level of Type with the smaller sample size (pharmaceuticals). The probability of observing an absolute difference from the mean midrank that exceeds the absolute value of S minus the mean of the midranks is 0.0005. This is a two-sided test for a difference in location and supports rejecting the hypothesis that profits do not differ by type of company.
In this example, the nonparametric tests are more appropriate than the normality-based ANOVA test or the unequal variances t test. The nonparametric tests are resistant to the large value in row 32 and do not require the assumption of normality.