Example to Evaluate the Loss of Planned Runs
Use the Compare Design platform to assess the impact of two lost design runs.
An experiment was conducted to explore the effect of three factors (Silica, Sulfur, and Silane) on tennis ball bounciness (Stretch). The goal of the experiment is to develop a predictive model for Stretch. A 15-run Box-Behnken design was selected using the Response Surface Design platform. After the experiment, the researcher learned that the two runs where Silica = 0.7 and Silane = 50 were not processed correctly. These runs could not be included in the analysis of the data.
For this example, use the design in Bounce Data.jmp as the intended design. Then remove two runs from the design to generate an actual design. Use the Compare Design platform to evaluate the impact of the loss of two runs from the planned experiment.
1. Select Help > Sample Data Folder and open Design Experiment/Bounce Data.jmp.
The following steps exclude the two runs where Silica = 0.7 and Silane = 50 from the 15 run design. These are rows 3 and 7 in the data table.
2. Select rows 3 and 7, right-click in the highlighted area, and select Rows > Row Selection > Invert Row Selection.
3. Select Tables > Subset and click OK
4. Select DOE > Design Diagnostics > Compare Design.
5. Select Bounce Data to compare with Subset of Bounce Data.
6. Select Silica, Sulfur, and Silane as Source Columns for both designs.
7. Click OK.
You can now compare the two designs.
Power Analysis
For a power analysis continue with the following steps.
8. Enter 2 for the Anticipated RMSE. The power calculations assume an error term (Anticipated RMSE) of 1. From previous studies, you believe that the RMSE is approximately 2.
9. You are interested in detecting differences in the anticipated response that are on the order of 6 units across the levels of main effects, assuming that interaction and quadratic terms are not active. Set the Anticipated Coefficients to 3 for all model terms.
10. Click Apply Changes to Anticipated Coefficients
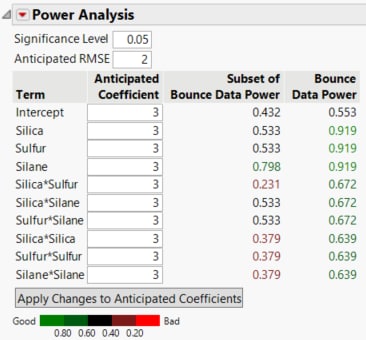
Figure 17.30 Power Analysis
The power values for the actual design are uniformly smaller than for the intended design. For Silica and Sulfur, the power of the tests in the intended design is almost twice the power in the actual design. For the Silica*Sulfur interaction, the power of the test in the actual design is 0.231, compared to 0.672 in the intended design. The actual design results in substantial loss of power in comparison with the intended design.
Prediction Variance Profile
Scroll down to the Prediction Variance Profile section.
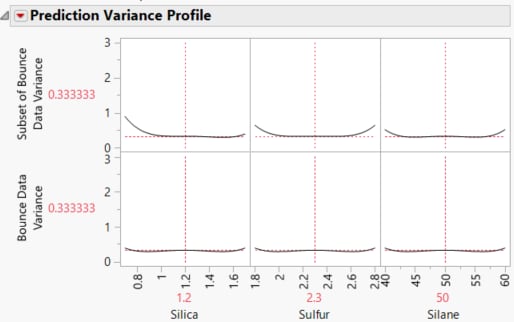
Figure 17.31 Prediction Variance Profiles: Actual Design (Top), Intended Design (Bottom)
The Prediction Variance Profile plots are of the relative prediction variance. You can explore the relative prediction variance in various regions of design space.
Both plots show the same relative prediction variance in the center of the design space. However, the variance for points near the edges of the design space are greater in the actual design than for the same points in the intended design.
11. Select Maximize Variance from the Prediction Variance Profile red triangle
The profilers identify that the maximum prediction variance occurs at Silica=0.7, Sulfur=1.8, and Silane=40. The maximum prediction variance is 1.396 for the intended design, and 3.021 for the actual design. Note that there are other combinations of settings where the prediction variance is maximized. The larger maximum prediction variance for the actual design means that predictions in parts of the design space are less accurate than they would have been had the intended design been conducted.
Fraction of Design Space Plot
Scroll down to the Fraction of Design Space section.
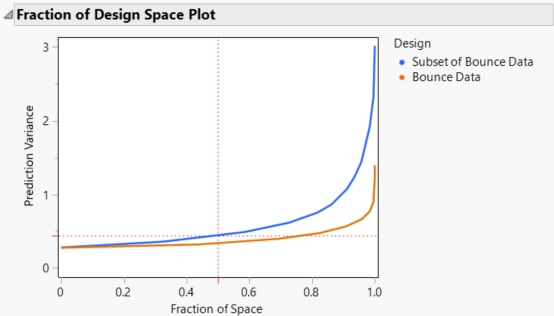
Figure 17.32 Fraction of Design Space Plots
The relative prediction variance for the actual design is greater than that of the intended design over the entire design space. The discrepancy increases with larger design space coverage.
Estimation Efficiency
Scroll to the Relative Estimation Efficiency section.
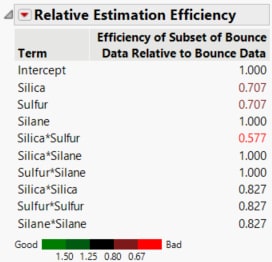
Figure 17.33 Relative Estimation Efficiency
The relative estimation efficiency for effects that contain silica or sulfur are lower in the actual design as compared to the intended design.
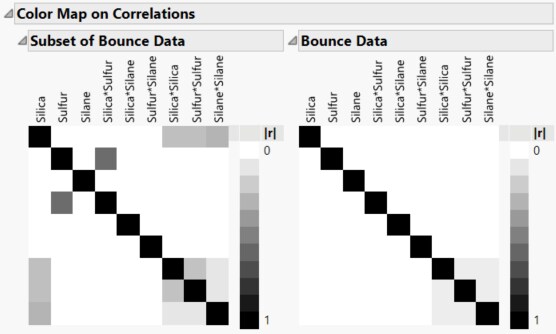
Color Map on Correlations
Scroll to the Color Map On Correlations section and open the color maps.
Figure 17.34 Color Map on Correlations, Intended Design (Left) and Actual Design (Right)
The two color maps show the effects in the Model. Each plot shows the absolute correlations between effects colored on a white to black intensity scale. Ideally, you would like zero or very small correlations between effects.The color map for the actual design shows more absolute correlations that are large than does the color map for the intended design. For example, the correlation between Sulfur and Silica*Sulfur is < .0001 for the intended design, and 0.5774 for the actual design.
Design Diagnostics
Scroll to the Design Diagnostics section.
Figure 17.35 Design Diagnostics
The intended design has lower efficiency values than the actual design. The results of the Design Evaluation analysis indicate that the two lost runs have had a negative impact on the design.
Note that both the number of runs and the model matrix factor into the calculation of efficiency measures. In particular, the D-, G-, and A- efficiencies are calculated relative to the ideal design for the run size of the given design. It is not necessarily true that larger designs are more efficient than smaller designs. For more information about how efficiency measures are defined, see Design Diagnostics.