Overview of the Fit Curve Platform
Some models are linear in the parameters (for example, a quadratic or other polynomial); others can be transformed to be such (for example, when you use a log transformation of x). The Fit Model or Fit Y by X platforms are more appropriate in these situations. An example in “Example of a Regression Analysis Using Fit Model” in Fitting Linear Models shows a significant linear relationship between oxygen uptake and time spent running. For more information about Fit Model, see “Model Specification” in Fitting Linear Models. For more information about Fit Y by X, see “Introduction to Fit Y by X” in Basic Analysis.
The Fit Curve platform enables you to fit models that are nonlinear in the parameters. The following are examples of equations for linear and nonlinear functions.
Linear function: 
Nonlinear function: 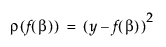
The Fit Curve platform provides predefined models, such as polynomial, logistic, probit, Gompertz, exponential, peak, pharmacokinetic, rate, and dissolution models. Specifying a grouping variable lets you estimate separate model parameters for each level of the grouping variable. The fitted models and estimated parameters can be compared across the levels of the grouping variable. There is also a set of options to compare dissolution profiles, with options for both parametric and nonparametric techniques.
Fit Curve also enables you to build a model to create the prediction formula. Then you set upper and lower parameter limits in Nonlinear. See “Example of Setting Parameter Limits”. In JMP Pro, you can also specify a set of supplementary variables and fit a generalized regression model within the Fit Curve platform to determine how these variables affect the response.