Result Table
Marker Annotation Position
This column lists the chromosomal location of each marker, provided you specify an annotation table listing the chromosomal locations of the markers. If no position information is supplied, the column number of each marker in the input JMP table is listed instead.
With Marker Annotation Position
This column lists the chromosomal location of each comparison marker, provided you specify an annotation table listing the chromosomal locations of the markers. If no position information is supplied, the column number of each comparison marker in the input JMP table is listed instead.
Distance between Marker Pairs
This column lists the distance between pairs of markers. If no position information is supplied, the number of columns between each comparison marker in the input JMP table is listed instead.
Count
The total number of individuals observed for each marker.
Missing Proportion
The proportion of the individuals missing data for each marker or pair of markers.
Genotype Count
The number of genotypes observed for each marker.
Allele Count
The number of alleles observed for each marker.
Minor Allele
The allele at each marker that occurs less frequently.
Most Common Allele Coded as Zero
The allele at each marker that occurs most frequently. Individuals homozygous for this allele are coded as 0 for that marker.
Minor Allele Frequency (MAF)
The MAF represents the proportion of the minor allele for each marker in the observed population. Assuming a biallelic marker locus M with alleles M1 and M2. A sample of N individuals of even ploidy k can therefore have k + 1 different genotypes at the locus. The number of individuals with i (i = 0, 1, 2, …, k) copies of allele M1 and j (j = 0, 1, 2, …, k) copies of allele M2 is denoted by Nij. The number n1 of copies of allele M1 can be found directly by summation: n1 = 0 × N00 + 1 × N10 + 2 × N20 + … + k × Nk0. The sample frequency of allele M1 is written as p1 = n1 / (k × n), frequency of allele M2 is written as p2 = 1 - p1, and the sample frequency for each genotype carrying u copies of allele M1 and v copies of allele M2 is written as Pij = Nij / n.
Polymorphism Information Content (PIC)
The PIC (Botstein et al., 1980; Hilderbrand, Torney, and Wagner, 1992) measures the probability of differentiating the allele transmitted by a given parent to its child given the marker genotype of father, mother, and child.
Heterozygosity (HET)
The heterozygosity, sometimes called the observed heterozygosity, is simply the proportion of heterozygous individuals in the observed population.
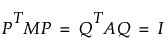
Allelic Diversity
The allelic diversity, sometimes called the expected heterozygosity, is the expected proportion of heterozygous individuals in the data set when HWE holds.
Degrees of Freedom for HWE
The HWE degrees of freedom are calculated using the formula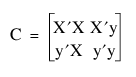 
, where k is the number of alleles found for a given marker that is being tested.
Chi-Squared for HWE
Under ideal population conditions, the two alleles an individual receives, one from each parent, are independent, so that Pii = p12, Pjj = p22 and Pij = 2p1 p2 (i and j = 0, 1, 2, …, k). The factor of 2 for heterozygotes recognizes the fact that M1 / M2 and M2 / M1 genotypes are generally indistinguishable. This statement about allelic independence within loci is called Hardy-Weinberg equilibrium (HWE). Forces such as selection, mutation, and migration in a population or nonrandom mating can cause departures from HWE. The chi-square goodness-of-fit test can be used to test markers for HWE (null hypothesis of Pii = p12, Pjj = p22, and Pij = 2p1 p2) is:
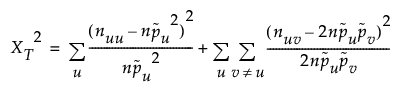
Chi-Squared for LD (ChiSQLD)
The chi-square statistic provides an estimate of the strength of the measures of linkage disequilibrium using the composite linkage disequilibrium (CLD) coefficient (Weir 1979). This method does not require the assumption of HWE and uses only allele and two-locus genotype frequencies.
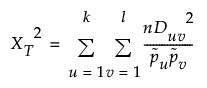
For biallelic markers, k and l = 2, and this test has 1 degree of freedom.
Composite LD (D)
The measure of the composite linkage disequilibrium (CLD) coefficient (Weir 1979), which does not assume HWE, and is written as follows: D12 = p12 + p1/2 - 2p1 p2, where:
– p12 is the frequency of gamete M1 M2
– p1/2 is the joint frequency of alleles M1 and M2 at two different gametes
– p1 and p2 are the frequencies of alleles M1 and M2 at two loci [Weir 1996]
Standardized Composite LD (D’)
The ratio of D to Dmax (Zaykin, 2004).
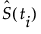
LD Correlation Coefficient (r)
A correlation coefficient assuming values from -1 to 1 indicator variables indicating the presence of the two loci.
P-value associated measures
4 columns of p-value-associated measures (PValue, Logworth (log10 p-value), FDR PValue (False Discovery Rate p-value), and FDR Logworth) of the strength of the chi-square test for Hardy-Weinberg Equilibrium and/or linkage disequilibrium.