Statistical Details for Odds Ratios
This section contains details for the odds ratios computed in the Fit Model platform.
For two response levels, the logistic regression model is specified as follows:
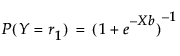where r1 and r1 are the two response levels
Therefore, the odds are defined as follows:
Note that exp(βi(Xi + 1)) = exp(βiXi) exp(βi). This shows that if Xi changes by a unit amount, the odds is multiplied by exp(βi), which is labeled as the unit odds ratio. As Xi changes over its whole range, the odds are multiplied by exp((Xhigh - Xlow)βi), which is labeled as the range odds ratio. For binary responses, the log odds ratio for flipped response levels involves only changing the sign of the parameter. Therefore, you might want the reciprocal of the reported value to focus on the last response level instead of the first.
Two-level nominal effects are coded 1 and -1 for the first and second levels, so range odds ratios or their reciprocals would be of interest.
Selecting the Odds Ratio option produces profile likelihood-based confidence intervals for the odds ratios unless the likelihood ratio tests are projected to take more than 20 seconds to complete. In this situation, the Odds Ratio option produces Wald-based confidence intervals for the odds ratios. The method used for computing confidence intervals for the odds ratios is noted at the bottom of the Odds Ratios report.