The Singular Value Decomposition
The singular value decomposition (SVD) enables you to express any linear transformation as a rotation, followed by a scaling, followed by another rotation. The SVD states that any n by p matrix X can be written as follows:
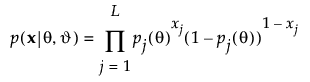
Let r be the rank of X. Denote the r by r identity matrix by Ir.
The matrices U, Diag(Λ), and V have the following properties:
U is an n by r semi-orthogonal matrix with U′U = Ir
V is a p by r semi-orthogonal matrix with V′V = Ir
Diag(Λ) is an r by r diagonal matrix with positive diagonal elements given by the column vector Λ = (λ1, λ2, ..., λr)′ where λ1 ≥ λ2 ≥ ... ≥ λr > 0.
The λi are the nonzero singular values of X.
The following statements relate the SVD to the spectral decomposition of a square matrix:
• The squares of the λi are the nonzero eigenvalues of X′X.
• The r columns of V are eigenvectors of X′X.
Note: There are various conventions in the literature regarding the dimensions of the matrices U, V, and the matrix containing the singular values. However, the differences have no practical impact on the decomposition up to the rank of X.
For more information about singular value decomposition, see Press et al. (1998, Section 2.6).
The Covariance Matrix
This section describes how the eigenvectors and eigenvalues of a covariance matrix can be obtained using the singular value decomposition (SVD). When the matrix of interest has at least one large dimension, calculating the SVD is much more efficient than calculating its covariance matrix and its eigenvalue decomposition.
Let n be the number of observations and p the number of variables involved in the multivariate analysis of interest. Denote the n by p matrix of data values by X.
The SVD is usually applied to standardized data. To standardize a value, subtract its mean and divide by its standard deviation. Denote the n by p matrix of standardized data values by Xs. Then the covariance matrix of the standardized data is the correlation matrix for X and is defined as follows:
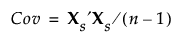
The SVD can be applied to Xs to obtain the eigenvectors and eigenvalues of Xs′Xs. This allows efficient calculation of eigenvectors and eigenvalues when the matrix X is either extremely wide (many columns) or tall (many rows). This technique is the basis for Wide PCA. See “Principal Components Report”.
The Inverse Covariance Matrix
Some multivariate techniques require the calculation of inverse covariance matrices. This section describes how the SVD can be used to calculate the inverse of a covariance matrix.
Denote the standardized data matrix by Xs and define S = Xs′Xs. The singular value decomposition enables you to write S as follows:
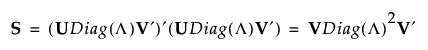
If S is of full rank, then V is a p by p orthonormal matrix, and you can write S-1 as follows:
If S is not of full rank, then Diag(Λ)-1 can be replaced with a generalized inverse, Diag(Λ)+, where the diagonal elements of Diag(Λ) are replaced by their reciprocals. This defines a generalize inverse of S as follows:
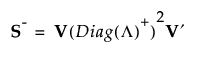
This generalized inverse can be calculated using only the SVD.
For more information about the application of the SVD for wide linear discriminant analysis, see “Wide Linear Discriminant Method”.
Calculating the Singular Value Decomposition
In the Multivariate Methods platforms, JMP calculates the SVD of a matrix following the method suggested in Golub and Kahan (1965). Golub and Kahan’s method involves a two-step procedure. The first step consists of reducing the matrix M to a bidiagonal matrix J. The second step consists of computing the singular values of J, which are the same as the singular values of the original matrix M. The columns of the matrix M are usually standardized in order to equalize the effect of the variables on the calculation. The Golub and Kahan method is computationally efficient.