Bayesian Parameter Estimates
Bayesian Parameter Estimates
In the Choice Model report, the Bayesian Parameter Estimates section provides results for model effects. This section is available only for Hierarchical Bayes models. The estimates are based on a Hierarchical Bayes fit that integrates the subject-level covariates into the likelihood function and estimates their effects on the parameters directly. The subject-level covariates are estimated using a Bayesian procedure combined with the Metropolis-Hastings algorithm. See Train (2001). Posterior means and variances are calculated for each model effect. The algorithm also provides subject-specific estimates of the model effect parameters. See Save Subject Estimates.
During the estimation process, each individual is assigned their own vector of parameter estimates, essentially treating the estimates as random effects and covariates. The vector of coefficients for an individual is assumed to come from a multivariate normal distribution with arbitrary mean and covariance matrix. The likelihood function for the utility parameters for a given subject is based on a multinominal logit model for each subject’s preference within a choice set, given the attributes in the choice set. The prior distribution for a given subject’s vector of coefficients is normal with mean equal to zero and a diagonal covariance matrix with the same variance for each subject. The covariance matrix is assumed to come from an inverse Wishart distribution with a scale matrix that is diagonal with equal diagonal entries.
For each subject, a number of burn-in iterations at the beginning of the chain is discarded. By default, this number is equal to half of the Number of Bayesian Iterations specified on the launch window.
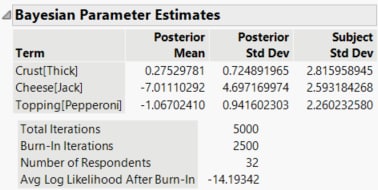
Figure 4.17 Bayesian Parameter Estimates Report
Term
The model term.
Posterior Mean
The parameter estimate for the term’s coefficient. For each iteration after the burn-in period, the mean of the subject-specific coefficient estimates is computed. The Posterior Mean is the average of these means.
Tip: Select the red triangle option Save Bayes Chain to see the individual estimates for each iteration.
Posterior Std Dev
The standard deviation of the means of the subject-specific estimates over the iterations after burn-in.
Subject Std Dev
The standard deviation of the subject-specific estimates.
Tip: Select the red triangle option Save Subject Estimates to see the individual estimates.
Total Iterations
The total number of iterations performed, including the burn-in period.
Burn-In Iterations
The number of burn-in iterations. This number is equal to half of the Number of Bayesian Iterations specified on the launch window.
Number of Respondents
The number of subjects.
Avg Log Likelihood After Burn-In
The average of the log-likelihood function, computed on values obtained after the burn-in period.