Example of a Structural Equation Model
Example of a Structural Equation Model
In this example, an employee in a human resources department wants to develop a survey to measure key workplace constructs. The example builds a confirmatory factor analysis model using the Structural Equation Models platform. You can use this model to analyze responses to a survey of 200 individuals regarding aspects of their workplace. The survey contains responses to 11 questions related to their job satisfaction. The confirmatory factor analysis model relates the answers of the survey questions to the latent variables of leadership characteristics, role conflict, and overall job satisfaction.
1. Select Help > Sample Data Folder and open Job Satisfaction.jmp.
2. Select Analyze > Multivariate Methods > Structural Equation Models.
3. Select Support_L through Supervisor_S and click Model Variables.
4. Click OK.
The Structural Equation Models report Model Specification outline appears.
Create Latent Variables
5. In the To List, select Support_L through Interact_L. Type Leadership in the box below the To List, and click the add latent ![]() button.
button.
6. In the To List, select Person_C through Inter_C. Type Conflict in the box below the To List, and click the add latent ![]() button.
button.
7. In the To List, select General_S through Supervisor_S. Type Satisfaction in the box below the To List, and click the add latent ![]() button.
button.
Add Covariances and Fit the Model
8. In both the From List and the To List, select Leadership, Conflict, and Satisfaction. Click the bidirectional arrow ![]() button.
button.
9. In the text box below Model Name (in the top left of the Model Specification report), type 3-Factor CFA.
10. Click Run.
11. (Optional.) Click the red triangle next to Structural Equation Model: 3-Factor CFA and select Path Diagram Settings > Layout > Top to Bottom.
12. (Optional.) Click the gray disclosure icon next to Parameter Estimates.
Closing the Parameter Estimates report enables you to see the entire path diagram.
13. Right-click the path diagram and select Show > Show Estimates > Standardized.
The numbers in the Path Diagram now represent the standardized parameter estimates for the model.
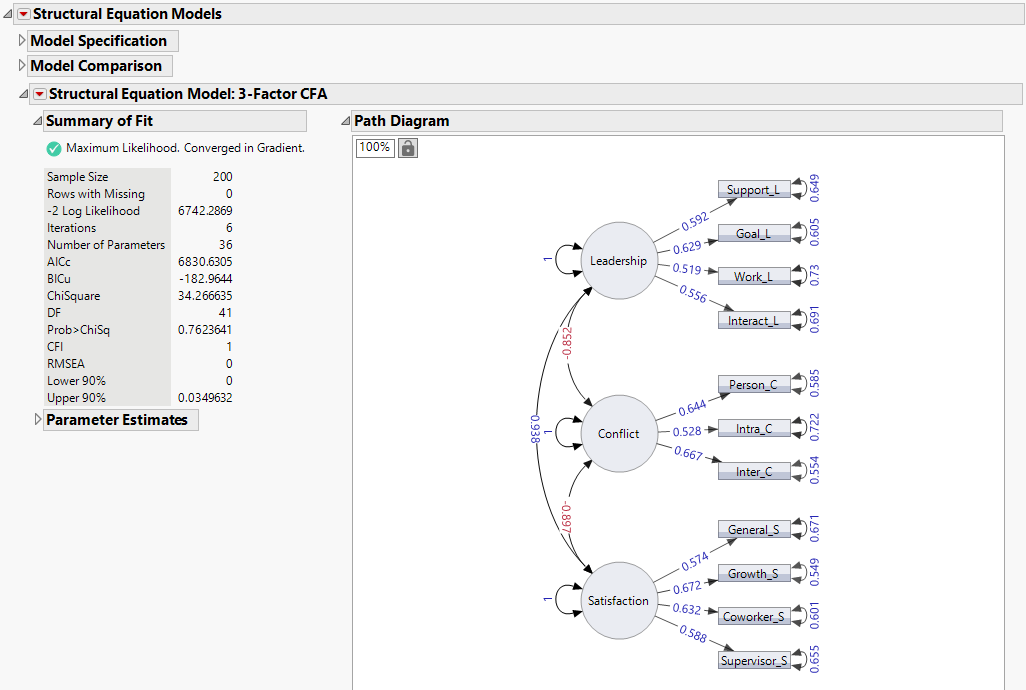
Figure 8.2 Structural Equation Model Report
The chi-square statistic for this model, listed in the Summary of Fit report, is 34.27 with 41 degrees of freedom. Note that the corresponding p-value is 0.7624, which is not significant. This indicates that there is not evidence to reject the null hypothesis that the model fits well. Therefore, you conclude that this model fits the data reasonably well.
The chi-square value depends on the sample size, and thus, some well-fitting models can still produce a significant chi-square value. The comparative fit index (CFI) and root mean square error of approximation (RMSEA) provide additional guidance for determining model fit. These indices are bounded between 0 and 1. CFI values greater than 0.90 and RMSEA values less than 0.10 are preferred (Browne and Cudeck 1993; Hu and Bentler 1999). Here, the CFI of 1 and RMSEA of 0 indicate an excellent fit. You conclude that the survey is a good instrument for measuring the latent variables for leadership, conflict, and satisfaction.
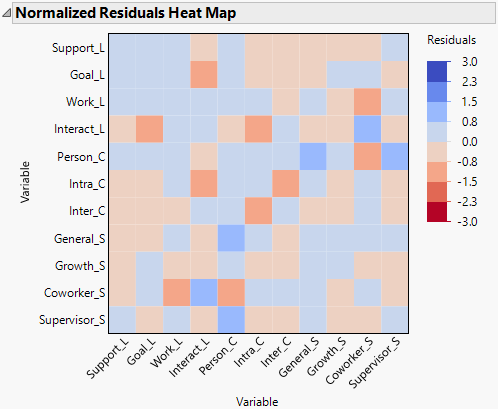
14. Click the red triangle next to Structural Equation Model: 3-Factor CFA and select Heat Maps > Normalized Residuals Heat Map.
Figure 8.3 Normalized Residuals Heat Map
The Normalized Residuals Heat Map has no values that exceed 2.0 units in the positive or negative direction; this is further evidence that the model fits the data well. The residuals can also diagnose ill-fitting models at a more granular level. The normalized residuals in this model do not show evidence of local misfit.