Example of a Two-Factor Nested Random Effects Model
Use the Standard Least Squares personality of the Fit Model platform to fit a two-factor nested random effects model. As part of a measurement systems analysis study, 24 randomly chosen parts are measured. These parts are evenly divided among the six operators who typically measure these parts. Each operator makes three independent measurements of each of the four assigned parts.
Since each part is measured by one specific operator, Part is nested within Operator. Since the parts are a random sample of production, Part is considered a random effect. Since these specific six operators are of interest, Operator is treated as a fixed effect. Specify the appropriate model.
1. Select Help > Sample Data Folder and open Variability Data/2 Factors Nested.jmp.
2. In the data table, click the green arrow next to Variability Chart - Nested table script.
3. Click the Variability Gauge Analysis for Y red triangle, deselect Show Range Bars, and select Show Group Means.
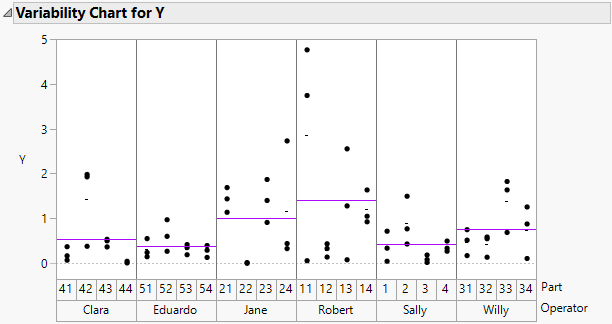
Figure 4.36 Variability Chart for Y
The variability chart shows the three measurements by each Operator on each of four parts. Horizontal lines show the mean measurement for each Operator.
4. Select Analyze > Fit Model.
5. Select Y and click Y.
6. Select Operator and Part and click Add.
7. To nest Part within Operator: In the Construct Model Effects list, select Part. In the Select Columns list, select Operator.
8. Click Nest.
9. With Part[Operator] highlighted in the Construct Model Effects list, select Attributes > Random Effect.
10. Click Run.
11. Click the Response Y red triangle and select Factor Profiling > Profiler.
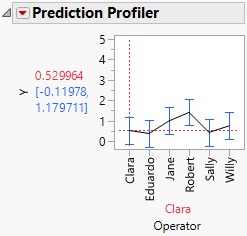
Figure 4.37 Prediction Profiler
The Prediction Profiler shows the predicted response for each operator. The vertical dashed red line set at Clara indicates that Clara’s predicted response is 0.530. You can see the correspondence between the model predictions given in the Prediction Profiler plot and the raw data in the Variability Chart.
This plot shows the predicted measurements for each Operator with Part nested within operator and as a random effect. If you are also interested in the variability of the part measurements themselves, estimation of the variance component associated with Part would be an appropriate analysis.