Example of Fitting Simple Survival Distributions
This section contains examples of fitting simple survival distributions in the Nonlinear platform.
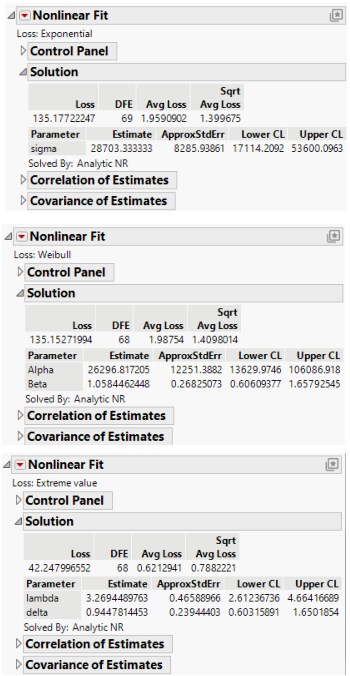
Exponential, Weibull, and Extreme-Value Loss Function
You can use the Nonlinear platform to fit exponential, Weibull, and extreme value loss functions to failure time data. The data in this example are from a study of 70 diesel fans that accumulated a total of over 300 thousand hours in service. The fans were placed in service at different times. The response is failure time of the fans or run time at censoring.
1. Select Help > Sample Data Folder and open Reliability/Fan.jmp.
Tip: To view the formulas for the loss functions, in the Fan.jmp data table, right-click the Exponential, Weibull, and Extreme value columns and select Formula.
2. Select Analyze > Specialized Modeling > Nonlinear.
3. Select Exponential and click Loss.
4. Click OK.
5. Make sure that the Loss is Neg LogLikelihood check box is selected.
6. Click Go.
7. Click Confidence Limits.
8. Repeat these steps, but select Weibull and Extreme value instead of Exponential.
Figure 15.28 Nonlinear Fit Results
Lognormal Loss Function
The lognormal distribution is useful when the range of the data is several powers of e. The lognormal loss function can be very sensitive to starting values for its parameters. Because the lognormal distribution is similar to the normal distribution, you can create a new variable that is the natural log of Time and use Distribution to find the mean and standard deviation of this column. Then, use those values as starting values for the Nonlinear platform. In this example, the mean of the natural log of Time is 4.72 and the standard deviation is 0.35.
1. Select Help > Sample Data Folder and open Reliability/Locomotive.jmp.
Tip: To view the formula for the loss function, in the Locomotive.jmp data table, right-click the logNormal column and select Formula.
2. Select Analyze > Specialized Modeling > Nonlinear.
3. Select logNormal and click Loss.
4. Click OK.
5. Type 4.72 in the box next to Mu.
6. Type 0.35 in the box next to sigma.
7. Click Go.
8. Click Confidence Limits.
Figure 15.29 Solution Report
The maximum likelihood estimates of the lognormal parameters are 5.11692 for Mu and 0.7055 for Sigma. The corresponding estimate of the median of the lognormal distribution is the antilog of 5.11692 (e5.11692), which is approximately 167. This represents the typical life for a locomotive engine.