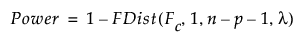Power for a Single Parameter
This section describes how power for the test of a single design parameter is computed. Use the following notation:
X
The model matrix. See “Statistical Details for Nominal Effects Coding” in Fitting Linear Models for information about the coding for nominal effects. Also, See Model Matrix.
Note: You can view the model matrix by running Fit Model. Then select Save Columns > Save Coding Table from the red triangle menu for the main report.
βι
The parameter corresponding to the term of interest.
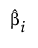
The least squares estimator of βi.
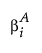
The Anticipated Coefficient value. The difference that you want to detect is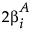 
.
The variance of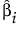 
is given by the ith diagonal entry of 
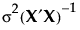, where σ2 is the error variance. Denote the ith diagonal entry of 
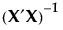by 
.
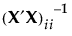The error variance, σ2, is estimated by the MSE, and has n − p − 1 degrees of freedom, where n is the number of observations and p is the number of terms other than the intercept in the model. If n − p − 1 = 0, then JMP sets the degrees of freedom for the error to 1. This allows the power to be estimated for parameters in a saturated design.
The test of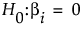 
is given by the ratio:
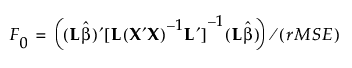
or equivalently by the following equation:
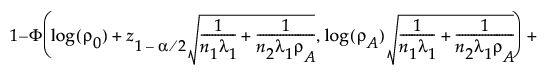
Under the null hypothesis, the test statistic F0 has an F distribution on 1 and n − p − 1 degrees of freedom.
If the true value of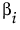 
is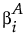 
, then F0 has a noncentral F distribution with noncentrality parameter given by the following equation:
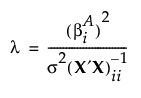
To compute the power of the test, first solve for the α-level critical value Fc:
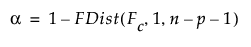
Then calculate the power as follows:
