Reliability Life Testing
Use the Reliability Life Test Interval Explorer to explore the sample size, study length, or precision needed for a reliability life test. Select DOE > Sample Size Explorers > Reliability > Reliability Life Testing.
Reliability life tests are used to estimate failure times and failure probabilities of a product. The Reliability Life Test explorer uses expected confidence intervals to define the precision of the estimates. These estimates are based on a fitted failure distribution.
Interval Explorer for Parametric Reliability Life Test Planning Settings
Set study assumptions and explore sample sizes using the radio buttons, text boxes, and menus. The profiler updates as you make changes to the settings. Alternatively, change settings by dragging the cross hairs on the profiler curves.
Interval Type
Lower Bound
Specifies a one-sided lower interval.
Upper Bound
Specifies a one-sided upper interval.
Interval
Specifies a two-sided interval.
Preliminary Information
Confidence Level
Specifies the confidence level, 1 - Alpha. The default alpha level is 0.05 for a 95% confidence interval.
Distribution
The assumed failure distribution. Distributions available are: Weibull, Lognormal, Frechet, and Loglogistic. For more information about these distributions, see Statistical Details for the Life Distribution Platform in Reliability and Survival Methods.
Censoring Time
The amount of time available to run the reliability test. Units surviving past this time are censored.
Quantile
(Available only for response type set to quantile.) The quantile to estimate, enter as a whole number.
Failure Time
(Available only for response type set to failure probability.) The time at which to calculate the failure probability.
Response Type
Quantile
Select to estimate the quantile of the life distribution.
Failure Probability
Select to estimate the probability of failing before a given time point
Interval Metric
Interval Ratio
The ratio of the upper to the lower interval limits.
Relative Width
(Available only when the Response Type option is set to Quantile.) The width of the interval relative to the magnitude of the estimate.
Absolute Width
(Available only when the Response Type option is set to Failure Probability.) The width of the interval.
Interval Explorer for Parametric Reliability Life Test Planning Profiler
The profiler enables you to visualize the impact of sample size assumptions on the interval calculations.
Solve for
Enables you to solve for the sample size.
Sample Size
The number of units to include in the reliability test.
Location Parameter
The location parameter for the failure distribution.
Note: The Location field is denoted Weibull α when the Distribution is set to Weibull.
Scale Parameter
The scale parameter for the failure distribution.
Note: The Scale field is denoted Weibull β when the Distribution is set to Weibull.
Interval Explorer for Parametric Reliability Life Test Planning Options
The Explorer red triangle menu and report buttons provide additional options:
Simulate Data
Opens a data table of simulated data based on the explorer settings. View the simulated response column formula for the settings used.
Make Data Collection Table
Creates a new data table that you can use for data collection. The table includes scripts to facilitate data analysis.
Save Settings
Saves the current settings to the Saved Settings table. This enables you to save a set of alternative study plans. See Saved Settings in the Sample Size Explorers.
Reset to Defaults
Resets all parameters and graphs to their default settings.
Help
Opens JMP online help.
Statistical Details for the Interval Explorer for Parametric Reliability Life Test Planning
The reliability test plan is designed to estimate either a quantile:
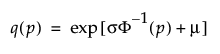
or a failure probability:
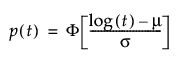
at a specified level of significance with an assumed failure time distribution and precision measure. Φ() is the standard cumulative distribution function of the assumed failure time distribution with location parameter μ and scale parameter σ. Wald confidence intervals and the precision measure define precision as a function of t (time) and n (sample size). Numerical methods are used to solve for the desired quantity.
For more information about calculations in JMP, see Barker (2011, Section 6)