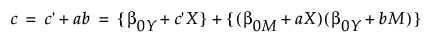Statistical Details for Mediation Analysis
This section describes the system of linear equations that are used in mediation analysis for the outcome (Y) and mediator (M) variables. The relationship between predictor (X) and mediator (M) and predictor (X) and outcome (Y) can be expressed as:
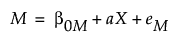
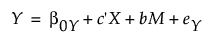
The first equation shows the effect of the predictor (X) on the mediator (M). For each unit increase in the predictor (X), the mediator (M) is expected to increase by a units. The second equation suggests that for two observations identical on mediator (M), a higher value in predictor (X) for one observation is projected to result in a c' unit change on outcome (Y). If the direct effect (c') shows a positive value, then as predictor (X) increases, outcome (Y) will probably increase as well. On the other hand, if the effect is negative, a rise in predictor (X) would likely result in a drop in outcome (Y).
These equations provide the foundational framework to measure the direct and indirect effects in the context of mediation analysis. They can be combined as follows:
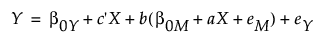
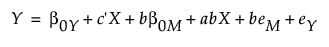
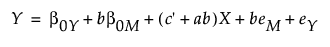
In this scenario, the following are true:
β0Y + bβ0M is the new intercept.
c' + ab is the new slope. This new slope is called total effect (c) and consists of direct (c') and indirect (ab) effects.
beM + eY is the new error term.
The total effect can be defined as follows:
Total Effect (c) = Direct Effect (c') + Indirect Effect (ab)