Statistical Details for Nonlinear Models
This section describes the type of model used in the Nonlinear Design platform. Denote the vector of n responses by Y = (Y1, Y2, ..., Yn)‘. A nonlinear model is defined by the following properties:
• The Yi are independent and identically distributed with an exponential family distribution.
• The expected value of each Yi given a vector of predictor values xi is a nonlinear function of parameters, θ. Denote this function as follows:
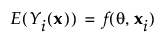
• Each Yi is expressed as follows:
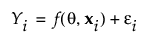
• The vector of errors, ε = (ε1, ε2, ..., εn)‘ has mean 0 and covariance matrix σ2I, where I is the n x n identity matrix.
Denote the matrix of first partial derivatives of the function f with respect to the parameters θ by X. Under general conditions, the least squares estimator of θ is asymptotically unbiased. The asymptotic covariance matrix is as follows:
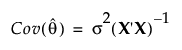
For the proof of this result, see Wu (1981) and Jennrich (1969).