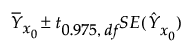Statistical Details for Prediction and Confidence Limits
This section describes the calculation of standard errors of prediction and confidence limits in the Partial Least Squares platform. Let X denote the matrix of predictors and Y the matrix of response values, which might be centered and scaled based on your selections in the launch window. Assume that the components of Y are independent and normally distributed with a common variance σ2.
Hoskuldsson (1988) observes that the PLS model for Y in terms of scores is formally similar to a multiple linear regression model. He uses this similarity to derive an approximate formula for the variance of a predicted value. See also Umetrics (1995). However, Denham (1997) points out that any value predicted by PLS is a non-linear function of the Ys. He suggests bootstrap and cross validation techniques for obtaining prediction intervals. The PLS platform uses the normality-based approach described in Umetrics (1995).
Denote the matrix whose columns are the scores by T and consider a new observation on X, x0. The predictive model for Y is obtained by regressing Y on T. Denote the score vector associated with x0 by t0.
Let a denote the number of factors. Define s2 to be the sum of squares of residuals divided by df = n - a -1 if the data are centered and df = n - a if the data are not centered. The value of s2 is an estimate of σ2.
Standard Error of Prediction Formula
The standard error of the predicted mean at x0 is estimated by the following:
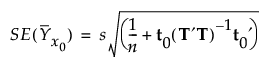
Mean Confidence Limit Formula
Let t0.975, df denote the 0.975 quantile of a t distribution with degrees of freedom df = n - a -1 if the data are centered and df = n - a if the data are not centered.
The 95% confidence interval for the mean is computed as follows:
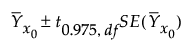
Indiv Confidence Limit Formula
The standard error of a predicted individual response at x0 is estimated by the following:
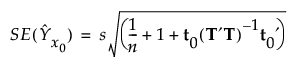
Let t0.975, df denote the 0.975 quantile of a t distribution with degrees of freedom df = n - a -1 if the data are centered and df = n - a if the data are not centered.
The 95% prediction interval for an individual response is computed as follows: