Statistical Details for Quantiles
This section describes how quantiles are computed in the Distribution platform.
To compute the pth quantile of n nonmissing values in a column, arrange the n values in ascending order and call these column values y1, y2, ..., yn. Compute the rank number for the pth quantile as r = (n + 1)p / 100. Define i as the integer part and f as the fractional part of r.
• If r ≥ n, the pth quantile is equal to the maximum value in the column.
• If r ≤ 1, the pth quantile is equal to the minimum value in the column.
• If r is an integer, the pth quantile is that rank’s corresponding value.
• If r is not an integer, the pth quantile is found by interpolation. The pth quantile, denoted qp, is defined as follows:
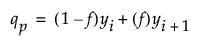
For example, suppose a data table has 15 rows and you want to find the 75th and 90th quantile values of a continuous column. After the column is arranged in ascending order, the ranks that contain these quantiles are computed as follows:
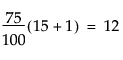 and
and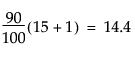
The value y12 is the 75th quantile. The 90th quantile is interpolated by computing a weighted average of the 14th and 15th ranked values as y90 = 0.6y14 + 0.4y15.