Statistical Details for Summary Statistics
This section contains statistical details for specific statistics in the Distribution Summary Statistics report. The mean, variance, skewness, and kurtosis are related to the first four moments of the probability distribution that describes the data. Moments are quantitative measures of the shape of a function.
Mean
The mean is the sum of the nonmissing values divided by the number of nonmissing values. If you assigned a Weight or Freq variable, the mean is computed as follows:
1. Each column value is multiplied by its corresponding weight or frequency.
2. These values are added and divided by the sum of the weights or frequencies.
Std Dev
The standard deviation measures the spread of a distribution around the mean. It is often denoted as s and is the square root of the sample variance, denoted s2.
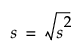
where
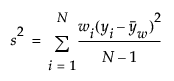
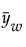= weighted mean
Std Err Mean
The standard error mean is computed by dividing the sample standard deviation, s, by the square root of N. In the launch window, if you specified a column for Weight or Freq, then the denominator is the square root of the sum of the weights or frequencies.
Skewness
Skewness is based on the third moment about the mean and is computed as follows:
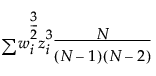where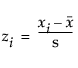 
and wi is a weight term (= 1 for equally weighted items).
Kurtosis
Kurtosis is based on the fourth moment about the mean and is computed as follows:
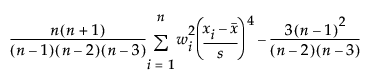
where wi is a weight term (= 1 for equally weighted items). Using this formula, the Normal distribution has a kurtosis of 0. This formula is often referred to as the excess kurtosis.