Statistical Details for the Agreement Statistic
This section contains details for the agreement statistic in the Contingency platform. Viewing the two response variables as two independent ratings of the n subjects, the Kappa coefficient equals +1 when there is complete agreement of the raters. When the observed agreement exceeds the amount of agreement expected just by chance, the Kappa coefficient is positive and its magnitude reflects the strength of agreement. Although unusual in practice, Kappa is negative when the observed agreement is less than the amount of agreement expected just by chance. The minimum value of Kappa depends on the marginal proportions, but it is always between -1 and 0.
The Kappa coefficient is computed as follows:
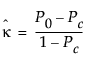where 
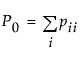and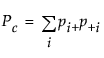 
Note that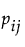 
is the proportion of subjects in the 
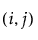th cell, such that 
.
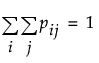The asymptotic variance of the simple kappa coefficient is estimated by the following:
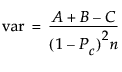where 
, 
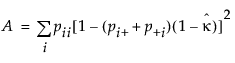and
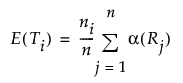
See Cohen (1960) and Fleiss et al. (1969).
For Bowker’s test of symmetry, the null hypothesis is that the probabilities in the two-by-two table satisfy symmetry (pij=pji).