Statistical Details for the Fit Line Option
In the Bivariate platform, the Fit Line option finds the parameters β0 and β1 for the straight line that fits the points to minimize the residual sum of squares. The model for the ith row is written yi = β0 + β1xi + εi.
The mean confidence limits for a linear fit are defined as follows:
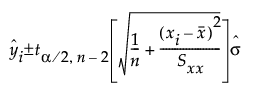
The individual confidence limits for a linear fit are defined as follows:
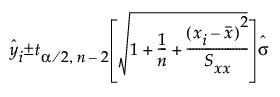
where
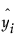 is the predicted value at xi, the ith observation
is the predicted value at xi, the ith observation
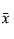 is the mean of the x variables
is the mean of the x variables
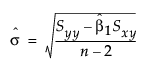
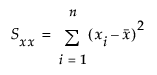
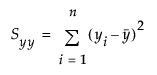
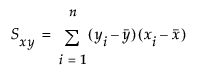
tα/2,n is the (α/2)th quantile of the central t-distribution with n–2 degrees of freedom
n is the sample size
Note: Use the Mean Confidence Limit Formula and the Individual Confidence Limit Formula options to save the limit formulas for any model fit to a new column in the data table. The formulas are saved in matrix formats.