 Statistical Details for the Gradient Descent Algorithm
Statistical Details for the Gradient Descent Algorithm
The Kullback-Leibler divergence used in the t-SNE method is minimized using a gradient descent algorithm based on the Barnes-Hut approximation (van der Maaten, 2014). The algorithm uses the following notation:
X = {x1, x2,..., xn} the original high-dimensional data with n data points
p = the perplexity parameter
T = the number of iterations
η = the learning rate
tinflate = the number of iterations after which the momentum value changes
α(t) = the momentum at iteration t, where α(t) = 0.5 for t ≤ tinflate and α(t) = 0.8 otherwise
Y(t) = {y1, y2,..., yn} the low-dimensional mapping solution at iteration t
The steps of the gradient descent algorithm are defined as follows:
1. Compute pj|i, the pairwise similarities in the high-dimensional space. Choose σi based on the specified perplexity p.
2. Calculate pij.
3. Set the initial solution Y(0) = {y1, y2,..., yn}, which is generated from a normal distribution with mean 0 and standard deviation 10-4.
4. For t = 1 to T:
– Compute qij, the pairwise similarities in the low-dimensional mapping.
– Compute the cost function:
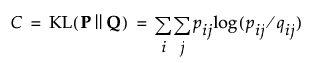
– Compute the gradient function, using the Barnes-Hut approximation:
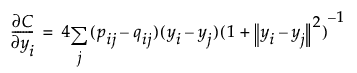
– Update the solution:
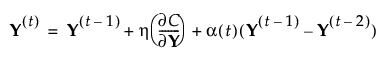
The algorithm stops when one of the following conditions is met:
• The maximum gradient value over i is less than the convergence criterion specified in the launch window.
• The maximum number of iterations, T, is reached.