Publication date: 06/27/2024
Statistical Details for the Inverse Correlation Matrix
In the Multivariate platform, the inverse correlation matrix provides useful multivariate information. The diagonal elements of the inverse correlation matrix, sometimes called the variance inflation factors (VIF), are a function of how closely the variable is a linear function of the other variables. Specifically, if the correlation matrix is denoted R and the inverse correlation matrix is denoted R-1, the diagonal element is denoted rii and is computed as follows:
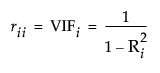
where Ri2 is the coefficient of variation from the model regressing the ith explanatory variable on the other explanatory variables. Thus, a large rii indicates that the ith variable is highly correlated with any number of the other variables.
Want more information? Have questions? Get answers in the JMP User Community (community.jmp.com).