Statistical Details for the Tests Report
This section contains details for the Tests report in the Contingency platform.
Rsquare (U)
Rsquare (U) is computed as follows:

The total negative log-likelihood is found by fitting fixed response rates across the total sample.
Test
The computations for the two chi-square tests are described in this section.
The likelihood ratio chi-square test statistic is computed as twice the negative log-likelihood for Model in the Tests table. Some books use the notation G2 for this statistic. The difference of two negative log-likelihoods, one with whole-population response probabilities and one with each-population response rates, is defined as follows:
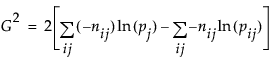 where
where 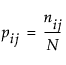 and
and 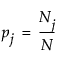
This formula can be more compactly written as follows:
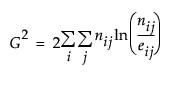
The Pearson chi-square test statistic is calculated by summing the squares of the differences between the observed and expected cell counts. The Pearson chi-square test exploits the property that frequency counts tend to a normal distribution in very large samples. The Pearson chi-square statistic is defined as follows:
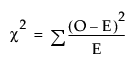
where O is the observed cell counts and E is the expected cell counts. The summation is over all cells. There is no continuity correction done here, as is sometimes done in 2 x 2 tables.