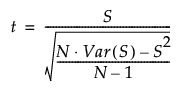Statistical Details for the Wilcoxon Signed Rank Test
The Wilcoxon signed-rank test in the Distribution platform can be used to test for the median of a single population or to test matched-pairs data for a common median. In the case of matched pairs, the test reduces to testing the single population of paired differences for a median of 0. The test assumes that the underlying population is symmetric.
The Wilcoxon test accommodates tied values. The test statistic is adjusted for differences of zero using a method suggested by Pratt. See Lehmann and D’Abrera (2006), Pratt (1959), and Cureton (1967).
Testing for the Median of a Single Population
• There are N observations:
X1, X2,..., XN
• The null hypothesis is:
H0: distribution of X is symmetric around m
• The differences between observations and the hypothesized value m are calculated as follows:
Dj = Xj - m
Testing for the Equality of Two Population Medians with Matched Pairs Data
A special case of the Wilcoxon signed-rank test is applied to matched-pairs data.
• There are N pairs of observations from two populations:
X1, X2,..., XN and Y1, Y2,..., YN
• The null hypothesis is:
H0: distribution of X - Y is symmetric around 0
• The differences between pairs of observations are calculated as follows:
Dj = Xj -Yj
Wilcoxon Signed-Rank Test Statistic
The test statistic is based on the sum of the signed ranks. Signed ranks are defined as follows:
• The absolute values of the differences, ⎟Dj⎟, are ranked from smallest to largest.
• The ranks start with the value 1, even if there are differences of zero.
• When there are tied absolute differences, they are assigned the average, or midrank, of the ranks of the observations.
Denote the rank or midrank for a difference Dj by Rj. Define the signed rank for Dj as follows:
• If the difference Dj is positive, the signed rank is Rj.
• If the difference Dj is zero, the signed rank is 0.
• If the difference Dj is negative, the signed rank is -Rj.
The signed-rank statistic is computed as follows:
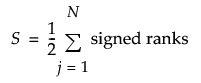
Define the following:
d0 is the number of signed ranks that equal zero
R+ is the sum of the positive signed ranks
Then the following holds:
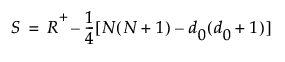
Wilcoxon Signed-Rank Test P-Values
For N ≤ 20, exact p-values are calculated.
For N > 20, a Student’s t approximation to the statistic defined below is used. Note that a correction for ties is applied. See Iman (1974) and Lehmann and D’Abrera (2006).
Under the null hypothesis, the mean of S is zero. The variance of S is given by the following:
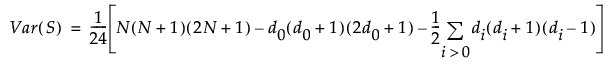
The last summation in the expression for Var(S) is a correction for ties. The notation di for i > 0 represents the number of values in the ith group of nonzero signed ranks. (If there are no ties for a given signed rank, then di = 1 and the summand is 0.)
The statistic t given by the following has an approximate t distribution with N - 1 degrees of freedom: