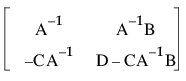Inverse()関数は、正則な正方行列の逆行列を戻します。Inverse()は、省略してInvと書くこともできます。行列Aにおいて、AとInverse(A)の積(よくA(A-1)と記載される)は、結果として単位行列を戻します。
A = [5 6, 7 8];
AInv = Inv( A );
A*A Inv;
A = [1 2, 3 4];
AInv = Inverse( A );
A*AInv;
AGA=A
GAG=G
GInverse()関数は、非正方行列を含めた任意の行列を引数にとり、特異値分解を使ってMoore-Penrose型の一般逆行列を求めます。この関数は、フルランクでない行列の逆行列を求めるときに便利です。次の方程式系を見てください。
A = [1 2 2, 2 4 4, 1 1 1];
B = [6, 12, 1];
Show( GInverse( A ) * B );
Solve()関数は、連立一次方程式の解を求めます。Solve()は、x = A-1bとなるベクトルxを求めます(ここで、Aは正方行列、bはベクトル)。この行列Aとベクトルbの行数は同じである必要があります。Solve(A,b)はInverse(A)*bと同じです。
A = [1 -4 2, 3 3 2, 0 4 -1];
b = [1, 2, 1];
x = Solve( A, b );
A*x;
Sweep()関数は、正方行列行列の部分(ピボットの逆行列を求めます。これをすべてのピボットに対して行うと、最終的には逆行列が求められます。通常、この行列は対角軸が0にならないよう、正定値行列(または負定値行列)である必要があります。Sweep()は、与えられた行列が正定値行列であるかどうかはチェックしません。正定値行列でない場合も、掃き出し法において、対角軸に0以外の値が現れる限り演算は続けられます。0(または0に近い値)が対角軸に現れた場合、その行と列を0にします。結果としてg2型の一般逆行列が求められます。
Sweep()の構文は次のようになります。
Sweep( E, [...] );
|
•
|
Aの位置の部分行列は逆行列になります。
|
|
•
|
|
•
|
Sweep()は逐次的で可逆的です。
|
•
|
A = Sweep( A, {i,j} )はA = Sweep( Sweep( A, i ), j )と同じで、 逐次的です。
|
|
•
|
A = Sweep( Sweep( A, i ), i )はAを元の値に復元します。これは可逆的です。
|
X’Xを引数としたSweep演算の結果は、次のようになります。
|
•
|
右上部はモデルY = Xb + eの最小2乗推定値
|
Sweep関数は、ステップワイズ回帰で必要な部分的な解を求める際に有効です。
E = [ 5 4 1 1, 4 5 1 1, 1 1 4 2, 1 1 2 4];
Sweep( E, [1, 2, 3, 4] );
Inverse( E ); // これらの結果は同じ
メモ: Sweep()の詳細と、逆行列を作成するGauss-Jordan法との関連については、Goodnight, J.H. (1979) “A tutorial on the SWEEP operator.” The American Statistician, August 1979, Vol. 33, No. 3. pp. 149-58を参照してください。
Sweep()については、第 “分散分析(ANOVA)の例”でさらに説明しています。
Det()関数は、正方行列の行列式を戻します。2 x 2行列の行列式は、下に示すように、対角線上の要素の積の差です。n x n行列の行列式は、(n - 1) × (n - 1)の行列式の重み和として再帰的に定義されます。逆行列を作成するには、行列の行列式が0以外でなければなりません。
F = [1 2, 3 5];
Det( F );