その他の数値関数

JSLでは、計算式エディタではあまり意味をなさない、関数の行列計算や数値微分も実行できます。微分については、以下で詳しく説明します。

行列に対しても、足し算や引き算などの基本的な演算を、行列をオペランドとして実行することができます。また、行列には、要素ごとの掛け算、要素ごとの割り算、行列同士の連結、要素の指定といった行列固有の演算子もいくつかあります。JSLスクリプトの行列を参照してください。

微分

JSLには、微分を求めるための関数は3つあります。Derivative、NumDeriv、およびNumDeriv2です。これらの関数は、計算式エディタでは用意されていません。

Derivative()関数は、第2引数に指定した変数で、第１引数に指定された式を微分した結果を戻します。この第2引数には1つの変数を指定することも、リストにして複数の変数を指定する（つまり、中括弧{ }で複数の変数名を囲む）こともできます。

メモ: Derivative()関数と同様の機能は、計算式エディタではコマンドとして用意されています。このコマンドは、計算式エディタの上部中央のドロップダウンリストにあります（キーパッドの上）。このコマンドを使用するには、式の中の1つの変数を強調表示（どの変数についての導関数を求めるかを指定）してから、メニューから［微分した式］コマンドを選びます。計算式全体が、強調表示された変数で微分した導関数に置き換わります。

スクリプトでこの関数を最も簡単に使用する方法は、変数を1つ指定する方法です。この例では、最初に数式による表記、次にJSLでの表記を示します。

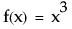の場合、第1次導関数はf ′(x)または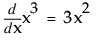です。

result = Derivative( x ^ 3, x );

Show( result );

result = 3 * x ^ 2

ある１つの式から複数の変数に対する導関数を効率的に求めたい場合は、リストに複数の変数を指定してください。一時変数に分割された元の式と、その導関数の式を含むリストが結果として戻されます。必要に応じて、導関数で用いる部分式が、一時変数に割り当てられます。

次の例は、3つの変数が含まれている式の例です。3つの変数をリストに入れると、それぞれの変数に対する第1次導関数を戻します。結果は、元の式と、要求した順に並べた導関数を含むリストになります。ただし、この例において、JMPが式x^2を格納するための一時的な変数T#1を作成し、この一時的な変数を使って計算を省略していることに注意してください。

result2 = Derivative( 3 * y * x ^ 2 + z ^ 3, {x, y, z} );

Show( result2 );

result2 = {3 * y * (T#1 = x ^ 2) + z ^ 3, 6 * x * y, 3 * T#1, 3 * z ^ 2}

第2次導関数をとるには、第3引数としてもう1つ変数を指定します。第2引数と第3引数は、どちらもリストでなければなりません。JMPは、元の式、第1次導関数、そして第2次導関数の順番で結果を含んだリストを戻します。

second = Derivative( 3 * y * x ^ 2, {x}, {x} );

Show( second );

second = {3 * y * x ^ 2, 6 * x * y, 6 * y}

second = Derivative( 3 * y * x ^ 2, {y}, {y} );

Show( second );

second = {3 * y * (T#1 = x ^ 2), 3 * T#1, 0}

second = Derivative( 3 * y * x ^ 2, {y}, {x} );

Show( second );

second = {3 * y * (T#2 = x ^ 2), 3 * T#2, 6 * x}

Num Deriv()は、数値微分を行うための関数です。第1引数と、それに小さい値（Δ）を足した値に対する関数値を計算し、その差をΔで割ることにより、1次微分の値を求めます。Num Deriv2()は、同様の方法で2次微分の値を数値的に求めます。これらの関数は、非線形モデルで内部的に使用されますが、JSLで直接利用することは少ないでしょう。これらの関数は変数では微分せず、関数に対する引数についてのみ微分することに注意してください。xについて微分するためには、xを、式の内部に埋め込まれている記号ではなく、関数の中の引数の1つにする必要があります。

x = 3で、y = 3x2を微分するとします。このとき次のスクリプトを実行すると、間違いになります。

x = 3;

n = Num Deriv( 3 * x ^ 2 );

xを関数の中の引数にするのが、正しい方法です。

x = 3;

f = Function( {x}, 3 * x ^ 2 );

n = Num Deriv( f( x ), 1 );

18.000029999854

数式による表記と、JSLでの表記方法を例を挙げて検討してみましょう。

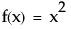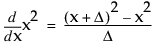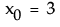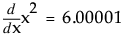の場合、という計算になります。では、です。

x = 3;

y = Num Deriv( x ^ 2 ); // または、y = Num Deriv( 3 ^ 2 );

6.0000099999513

もう少し例を挙げます。

x = Num Deriv( Sqrt( 7 ) ); // 0.188982168980445を戻す

y = Num Deriv( Normal Distribution( 1 ) ); // 0.241969514669371を戻す

z = Num Deriv2( Normal Distribution( 1 ) ); // -0.241969777547979を戻す

より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).