指標の計算式
被覆配列計画に対して計算される指標は、被覆度と多様度の2つです。被覆度と多様度の計算式は、組み合わせの制約の有無によって異なります。計算式では、次のような記号を使います。
uCvは、u個のものからv個を選ぶときの組み合わせの数
tは、計画の強度
Kは、因子の個数
M = KCt
i = 1, 2, ..., Mは、K個からt個を取り出す組み合わせ（射影）に対して振られる通し番号
vikは、k番目の因子の水準数
niは、i番目の射影（t個の因子への射影におけるi番目のもの）における、因子設定の一意な組み合わせの個数
piは、i番目の射影におけるvikの積
rは、計画全体における実験回数
制約のない計画
被覆度と多様度は、次のような計算式で求められます。
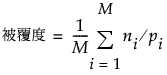
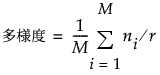
制約のある計画
JMPの「被覆配列」プラットフォームでは、t個の因子における水準の組み合わせに関して、いくつかの特定の組を許可しないようにすることもできます。そのとき、いくつかの組み合わせにおいて、因子の水準が欠測値になることもあります。なぜなら、特定のt個の因子に関して、制約を満たす組み合わせをまったく構成できない場合もあるからです。制約のある被覆配列では、被覆度と多様度は、可能な組み合わせから定義されます。制約のある計画の指標を計算するために、先ほどの計算式に対して、次のような要素も考慮されます。
aiは、t因子の水準から構成されたi番目の射影での因子設定の組み合わせのうち、制約により禁止されているものの個数
mは、制約を満たす因子設定の組み合わせが1つも存在しない射影の数
qiは、i番目の射影において、いずれかの因子が欠測値となる個数
ri = r - qi
M ′ = M - m
被覆度と多様度は、次のような計算式で求められます。
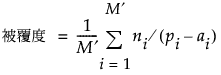
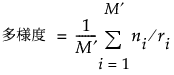
t因子の水準から作られる組み合わせに無効なものがなく（M′ = M）、また、欠測値がない（すべてのiに対してri = r）場合、制約のある計画の被覆度と多様度の定義は、制約のない計画のそれと同じになります。Morgan（2014）を参照してください。