公開日: 09/19/2023
「二変量の関係」プラットフォームの概要
2変数の関係を調べる
変数のペアについての分析には、「二変量の関係」プラットフォームを使用してください。「二変量の関係」プラットフォームでは、散布図・線形回帰・分散分析・多重比較・ロジスティック回帰・分割表などのグラフや統計分析が利用できます。実行できる分析の種類は、変数の尺度によって異なります。
「二変量の関係」起動ウィンドウは、次の4種類のプラットフォームのいずれかを開きます。
• 連続尺度のYと連続尺度のXを分析するには、「二変量」を使用します。
• 連続尺度のYとカテゴリカルなXを分析するには、「一元配置」(分散分析を含む)を使用します。
• カテゴリカルなYと連続尺度のXを分析するには、「ロジスティック回帰」を使用します。
• カテゴリカルなYとカテゴリカルなXを分析するには、「分割表」を使用します。
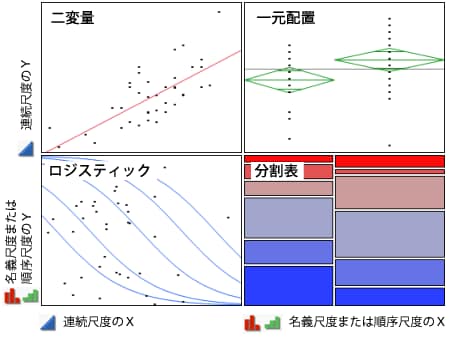
図4.1 4種類の分析
つまり、「二変量の関係」プラットフォームは、「二変量」・「一元配置」・「ロジスティック」・「分割表」という4つの分析プラットフォームで構成されています。
プラットフォーム | 尺度 | 説明 |
|---|---|---|
二変量 | X: 連続 Y: 連続 | 2つの連続変数における関係を分析します。二変量分析を参照してください。 |
一元配置 | X: 名義/順序 Y: 連続 | X変数のグループごとに、連続尺度のY変数の分布がどのように異なるかを分析します。一元配置分析を参照してください。 |
分割表 | X: 名義/順序 Y: 名義/順序 | X変数のグループごとに、カテゴリカルなY変数の分布がどのように異なるかを分析します。分割表分析を参照してください。 |
ロジスティック | X: 連続 Y: 名義/順序 | カテゴリカルなY変数の確率を、連続尺度のX変数にあてはめます。ロジスティック分析を参照してください。 |
より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).