「Passing-Bablokのあてはめ」レポート
「二変量」プラットフォームの［Passing Bablokのあてはめ］オプションは、Passing-Bablok手法を使って回帰モデルをあてはめます。Passing-Bablok回帰は、同じ対象を2つの異なる測定方法で測定した場合に、それら2つの測定方法を比較する目的で開発されました。この手法は、2つの変数の間の関係は1次式であり、かつ、強い相関があると仮定しています。散布図に、あてはめ線とY = Xの点線が追加されます。「Passing-Bablokのあてはめ」の赤い三角ボタンのメニューにある［Bland Altman分析］オプションは、対応のあるt検定およびBland-Altman分析を行います。
「Passing-Bablokのあてはめ」レポートは、3つの表で構成されます。
ノンパラメトリック: Kendallの順位相関係数(t)
Kendallのtを使ってX変数とY変数の間の相関を評価します。
X
X変数。
Y
Y変数。
Kendallのτ
X変数とY変数の相関を示すノンパラメトリックな指標。-1～1の値を取り、0に近い値は、X変数とY変数が独立であることを示唆します。
p値(Prob>|t|)
「X変数とY変数は独立である」という帰無仮説に対する仮説検定のp値。小さいp値は、X変数とY変数は独立ではないことを示唆しています。独立でない場合にのみ、Passing-Bablok法は適しています。
直線性の累積和検定
「直線性の累積和検定」表は、直線性の検定結果をまとめたものです。p値が小さい場合、直線性の帰無仮説は棄却されます。Passing-Bablok回帰は直線性を仮定しているので、直線性の帰無仮説が棄却された場合、Passing-Bablok回帰が適さないことを示唆します。
最大累積和
各点からPassing-Bablok回帰直線までの垂直距離に応じて並べられた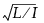
と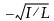
の値の累積和の最大絶対値。Iは、正の残差を持つ観測の個数、Lは、負の残差を持つ観測の個数です。また、プラスとマイナスのいずれにするかは、残差の符号で決められます。手法間に強い相関がある場合、IとLは等しくなります。そのため、多くの場合、累積和は+1と-1の和になります。最大累積和の値が小さいときは、Passing-Bablok回帰直線の上側と下側に均等に点が散らばっていることを示し、直線性の仮説が支持されます。
H
累積和検定の検定統計量。この検定統計量は、最大累積和を、残差が負になっている観測数に1を足した値の平方根で割ったものです。この検定統計量は、Kolmogorov-Smirnov分布に従います。
p値(Prob > H)
累積和検定のp値。小さいp値は、Passing-Bablok法が適切でない可能性を示唆します。
パラメータ推定値
「パラメータ推定値」表には、Passing-Bablok法による切片と傾きの推定値、およびその95%信頼区間が表示されます。
「対応のあるペア」レポート
「Passing-Bablokのあてはめ」の赤い三角ボタンのメニューにある［Bland Altman分析］オプションは、対応のあるt検定とBland-Altman分析を行います。対応のあるペアの詳細については、『予測モデルおよび発展的なモデル』の対応のあるペア分析を参照してください。
Bland-Altman分析
「Bland-Altman分析」表には、次の「値」・「標準偏差」・「信頼限界」が表示されます。
バイアス
X変数とY変数の差。「値」には差の平均が、「標準偏差」には差の標準偏差が表示されます。
許容範囲の限界
許容範囲（limits of agreement）の上限と下限です。これは、「差の平均」 ± z1-α/2×「差の標準偏差」です。