カテゴリカルな効果に対する検出力

この節では、カテゴリカルな効果全体の検定に対する検出力の計算方法を解説します。次のような表記を使用します。

X

計画行列（デザイン行列）。交絡行列を参照してください。

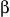
パラメータのベクトル。

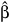
最小2乗法で求めたbの推定値。

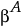
係数の予想値のベクトル。

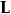
カテゴリカルな効果の検定を定義する行列。行列Lは、カテゴリカルな効果に対応するbを特定し、それらが0であるという帰無仮説を構成します。カテゴリカルな効果に対する検定の帰無仮説は、次のように表されます。

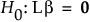
r

Lのランク。つまり、rは、カテゴリカルな効果の水準数から1を引いた値です。

メモ: 計画行列を表示するには、［モデルのあてはめ］を実行します。その後、レポートの赤い三角ボタンのメニューから［列の保存］>［コーディングのテーブルを保存］を選択します。

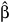の共分散行列は、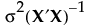で与えられます。ここで、σ2は誤差分散です。

誤差分散のσ2は、平均2乗誤差（MSE; Mean Squared Error）によって推定され、その自由度はn − p − 1です。ここで、nは標本サイズ、pは切片を除くモデル項の数です。n − p − 1 = 0の場合、誤差の自由度は1に設定されます。自由度を0に設定することにより、飽和計画でもパラメータに対する検出力を算出します。

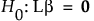の検定に対する検定統計量であるF値は、次のようになります。

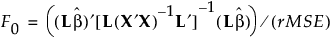
帰無仮説の下では、検定統計量F0は、分子自由度がrで、分母自由度がn − p − 1のF分布に従います。

もしbの真値が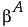である場合、F0は次のような非心パラメータを持つ非心F分布に従います。

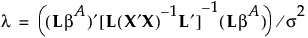
検定の検出力を求めるには、まず、有意水準がaである棄却値Fcを求めます。

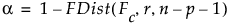
そして、次式で検出力を計算します。

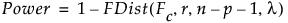
より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).