変化点検出の統計的詳細
このセクションでは、「多変量管理図」プラットフォームの［変化点の検出］オプションを詳しく取り上げます。ここでは、Sullivan and Woodall（2000）に沿って説明します。
仮定
平均ベクトルmi と共分散行列Si を持つ次元pの多変量分布をNp(mi,Si)とします。xiは、次のような分布に従うm（ここで、m > p）個の独立した観測だと仮定します。
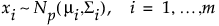
工程が安定しているなら、平均miと共分散行列Siは共通の値となり、xiがNp(m, S)の分布に従います。
時点m1と時点m1 + 1の間で、平均ベクトルと共分散行列のどちらか、または両方に1つの変化が生じたとしましょう。ここで、次のように仮定します。
• 時点1から時点m1まで、同じ平均ベクトルと同じ共分散行列(ma,Sa)になっている。
• 時点m1 + 1から時点mまで、同じ平均ベクトルと共分散行列(mb,Sb)になっている。
• 次のいずれかの処理が行われます。
– 平均が変化した場合。つまり、ma ¹ mbとなった場合。
– 共分散行列が変化した場合。つまり、Sa ¹ Sbとなった場合。
– 平均と共分散行列の両方が変化した場合。つまり、ma ¹ mb、およびSa ¹ Sbとなった場合。
概要
ここで採用されている尤度比検定の枠組みは、平均ベクトルと共分散行列のいずれか、または両方に生じた変化を検出するものです。尤度比検定統計量から、上側管理限界の近似値が1となるような、管理図の統計量が計算されます。この管理図の統計量は、m1の可能なすべての値に対してプロットされます。管理図の統計量が上側管理限界である1を超えた場合、それは、シフトが生じたことを示唆します。シフトが1つしか生じていないと仮定すると、そのシフトは、管理図の統計量が最大である時点の直後で生じたと考えられます。
尤度比検定統計量
最初のm1個の観測から求められる対数尤度関数の2倍の最大値は、次のように計算されます。
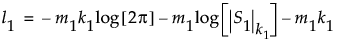
l1の式では、次のような表記を使用しています。
• S1は、最初のm1個の観測から求められた、共分散行列の最尤推定値です。
• k1 = Min[p,m1-1]は、p x pの行列S1のランクです。
• 
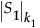という表記は、行列S1の一般化した行列式です。k1個の正の固有値ljの積です。
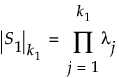
この一般化した行列式は、S1がフルランクである場合は、通常の行列式に等しくなります。
後に続くm2 = m - m1個の観測から求められる対数尤度関数の2倍の最大値をl2とし、m個すべての観測から求められる対数尤度の2倍の最大値をl0とします。l2とl0は、どちらもl1と同様の計算式で求められます。
尤度比検定統計量は、l1 + l2の和をl0と比較します。l1 + l2の和は、m1でシフトが生じていると仮定したときの対数尤度の2倍です。l0の値は、シフトがないと仮定したときの対数尤度の2倍です。l0がl1 + l2を大幅に下回る場合、工程は不安定な状態にあると考えられます。
変化が時点m1 + 1で始まるかどうかを検定する尤度比検定統計量は、次のようにして求めます。
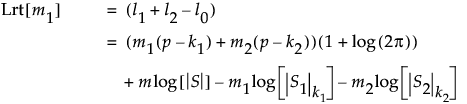
尤度比検定統計量の分布は、自由度がp(p + 3)/2のカイ2乗分布に近似的に従います。対数尤度比の値が大きい場合は、該当の時点における前後で工程には変化が生じたと考えられます。
管理図統計量
シミュレーションから、lrt[m1]の期待値は、期間内における時点の位置によって異なり、さらに、特にpとmに依存することがわかっています。Sullivan and Woodall（2000）を参照してください。
lrt[m1]の期待値の近似計算式は、シミュレーションから計算されます。期待値のpへの依存を弱める目的で、lrt[m1]は、その漸近期待値であるp(p + 3)/2で割られます。
lrt[m1]をp(p+3)/2で割ったものの期待値に対する近似値として、次の式が使われています。
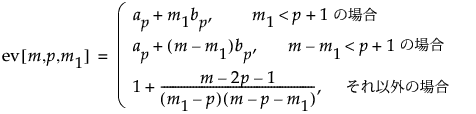
ここで
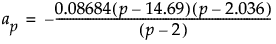
および
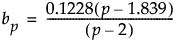
なお、p = 2で、m1 = 2またはm2 = 2の場合には、ev[m,p,m1] = 1.3505とします。
メモ: この近似式は、p > 12またはm < (2p + 4)の場合には近似がよくありません。そのような場合は、上記の近似式によってではなく、乱数シミュレーションによって近似の期待値を求めるべきです。
工程が安定していると仮定した場合に、誤って管理外であると判断する確率が約0.05であるときの上側管理限界の近似値は、次式で計算します。
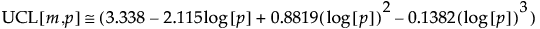
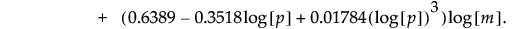
この計算式は、mとpに依存します。
変化点検出の統計量は、尤度比検定統計量の対数の2倍を、p(p + 3)、その期待値の近似値、および、その管理限界の近似値で割ったものとして定義されています。管理限界の近似値で割ることにより、算出された管理図の統計量の上側管理限界は1となります。最終的に、管理図の統計量は次式で計算されます。
