管理限界の統計的詳細
「モデルに基づく多変量管理図」プラットフォームでは、起動ウィンドウにて履歴データの行数が指定されていない場合は、すべてのデータが履歴データであるとみなされます。「モデルに基づく多変量管理図」プラットフォームの起動を参照してください。
T2
履歴データに対する上側管理限界（UCL; Upper Control Limit）は、ベータ分布に基づき、次のように計算されます。
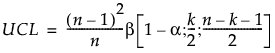
ここで
n = 履歴データの観測数
k = PCA成分またはPLS成分の個数
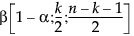= パラメータが
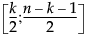であるベータ分布の(1−a)分位点
現在のデータに対するUCLは、F分布に基づき、次のように計算されます。
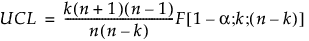
ここで
n = 履歴データの観測数
k = PCA成分またはPLS成分の個数
F(1−a; k; n−k) = F(k; n−k)分布の(1−a)番目の分位点
Xモデルまでの距離
PCAモデルおよびPLSモデルの場合、UCLはF分布に基づきます。PCAモデルの場合、Xモデルまでの距離のUCLは、次のように計算されます。
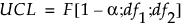
ここで
df1 = p−k
データが中心化されている場合は、df2 = (n−k−1)(p−k)、データが中心化されていない場合は、 (n−k)(p−k)
n = 履歴データの観測数
k = PCA成分の個数
p = 変数の個数
F(1−a; n−p−1; p−k) = F(n−p−1; p−k)分布の(1−a)番目の分位点
PLSモデルの場合、Xモデルまでの距離のUCLは、次のように計算されます。
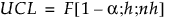
ここで
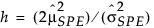
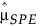= 履歴データでのSPEの標本平均
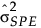= 履歴データでのSPEの標本分散
n = 履歴データの観測数
F(1−a; h; nh) = F(h; nh) 分布の(1−a)番目の分位点
SPE
PCAモデルの場合、SPEのUCLは、次のように計算されます。
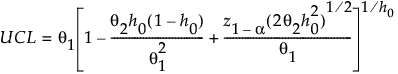
ここで
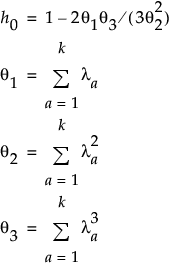
la = a番目の固有値
k = PCA成分の個数
z1−α = 標準正規分布の(1−a)番目の分位点
PCAモデルでのSPEに対する管理限界の詳細については、Jackson and Mudholkar（1979）を参照してください。
PLSモデルの場合、UCLは、カイ2乗分布に基づき、次のように計算されます。
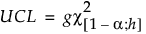
ここで
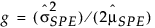
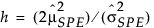
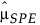= 履歴データでのSPEの標本平均
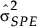= 履歴データでのSPEの標本分散
c2(1−a; h) = c2(h)分布の(1−a)番目の分位点
gパラメータとhパラメータは、モーメント法により推定されます。PLSモデルでのSPEに対する管理限界の詳細については、Nomikos（1995）を参照してください。