サブグループに分けたデータに対する多変量管理図の統計的詳細
「多変量管理図」プラットフォームを使用して、サブグループに分けた測定値を分析することができます。p個の変数を監視し、標本サイズnが1より大きいサブグループがm個得られたとします。T2統計量は、サブグループごとに計算され、プロットされます。T2統計量と上側管理限界（UCL; Upper Control Limit）の計算式は、目標統計量を求めたデータの種類によって異なります。フェーズI管理図の管理限界は、管理図上にプロットされたのと同じデータから計算されます。フェーズII管理図の管理限界は、履歴データから求めた目標統計量に基づいて計算されます。HotellingのT2管理図のT2統計量と管理限界の詳しい計算方法については、Montgomery（2013）を参照してください。
フェーズI管理図の計算
フェーズI管理図では、j番目のサブグループのT2統計量は、次式により計算されます。
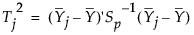
ここで
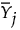は、j番目のサブグループにおける、p個の測定値を要素とする列ベクトルの、n個から計算される平均。
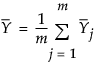はサブグループ平均の平均。
Sjは、j番目のサブグループにおける、n個の観測から計算された標本共分散行列。
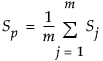は、群内共分散行列の平均として求めた、プールした共分散行列。
フェーズIの上側管理限界（UCL）は、次式により計算されます。
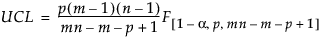
ここで
p = 変数の個数
n = 各サブグループの標本サイズ
m = サブグループの数
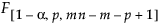= F
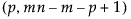分布の第(1–a)分位点
フェーズII管理図の計算
フェーズII管理図において、目標統計量を計算するのに用いた履歴データセットをXとします。j番目の観測におけるT2統計量は、次式により計算されます。
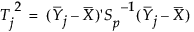
ここで
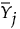は、j番目のサブグループにおける、p個の測定値を要素とする列ベクトルの、n個から計算される平均。
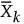は、履歴データから求めた、k番目のサブグループにおける、p個の測定値を要素とする列ベクトルの、n個から計算される平均。
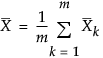は、データ全体の平均。
Skは、履歴データから求めた、k番目のサブグループにおける、n個の観測から計算された標本共分散行列。
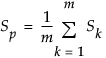は、群内共分散行列の平均として求めた、プールした共分散行列。
フェーズIIの上側管理限界（UCL）は、次式により計算されます。
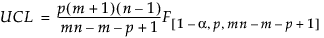
ここで
p = 変数の個数
n = サブグループの標本サイズ
m = 履歴データにおけるサブグループの数
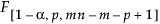= F
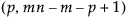分布の第(1–a)分位点
サブグループに分けたデータの検定統計量の加算性
独立した正規分布に従うmn個の観測から成る標本を、標本サイズがnである合理的なサブグループm個にグループ化したとします。ここで、j番目のサブグループにおける平均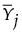
と目標値との距離をT2Mと表します。（このT2Mは、前節で求めた、サブグループ化されたデータにおけるT2です。）一方、各サブグループの個々のデータに関して、群内変動や、全体的な変動を表す、T2統計量も定義できます。これら3つのT2統計量には、平方和のように加算性があります。具体的には、m個のサブグループのそれぞれについて、次のような関係が成り立ちます。
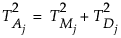
次の定義のすべてにおいて、Spは、フェーズIとフェーズIIのどちらの管理図かによって、これまでの節と同様に定義されます。また、mはフェーズIの管理図の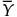
、フェーズIIの管理図の
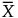とします。
j番目のサブグループの目標値からの距離は、次のように定義されます。
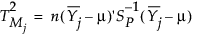
j番目のサブグループにおける群内変動は、次のように定義されます。
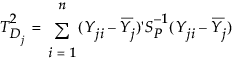
ここで、Yjiは第jサブグループにおけるi番目の列ベクトル（p個の測定値を要素としてもつ列ベクトル）です。
j番目のサブグループにおける全体的な変動は、次のように定義されます。
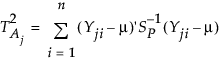
ここで、Yjiは第jサブグループにおけるi番目の列ベクトル（p個の測定値を要素としてもつ列ベクトル）です。
メモ: 「多変量管理図」の赤い三角ボタンのメニューから［T2乗の保存］や［T2乗の計算式の保存］オプションを選択すると各行に保存される値は、上記の3つの式で計算される、第i番目に対する結果です。