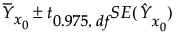予測値と信頼限界の統計的詳細
ここでは、「PLS回帰」プラットフォームにおける予測値の標準誤差および信頼限界の計算方法について説明します。Xを説明変数の行列、Yを応答変数の行列とします。これらは、起動ウィンドウでの選択内容に基づいて中心化・尺度化されます。Yの成分は、互いに独立で、共通の分散σ2である正規分布に従うと仮定します。
Hoskuldsson(1988)はスコアを説明変数としたYに対する回帰モデルとして見れば、PLSモデルは線形重回帰モデルと形式的に似ていると述べています。彼は、この類似性を使って、予測値の分散の近似式を紹介しています。Umetrics(1995)も参照してください。ただし、Denham(1997)は、PLSの予測値は、Yの非線形関数であると指摘しています。彼は、予測値の信頼区間を求めるのに、ブートストラップや交差検証の手法を推奨しています。「PLS回帰」プラットフォームでは、Umetrics(1995)で説明されている正規分布に基づく計算を用いています。
以下では、Xスコアの行列をTとし、Xの新しい観測値x0を考えます。Yに対する予測値は、Tに対するYの回帰モデルで算出されます。x0に対応したスコアベクトルをt0と記します。
aを因子の数とします。s2を、データが中心化されている場合は残差平方和をdf = n - a -1で除算したもの、データが中心化されていない場合は残差平方和をdf = n - aで除算したものとします。このs2は、σ2の推定値です。
平均の標準誤差
x0における応答変数の平均に対する標準誤差は、次式で推定されます。

平均に対する信頼区間の計算式
t0.975,dfを、データが中心化されている場合は自由度df = n - a -1のt分布の97.5%点、データが中心化されていない場合はdf = n - aのt分布の97.5%点とします。
平均の95%信頼区間は、次式で求められます。
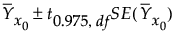
個々の値に対する信頼区間の計算式
x0における個々の応答値に対する標準誤差は、次式で推定されます。
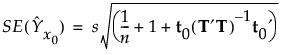
t0.975,dfを、データが中心化されている場合は自由度df = n - a -1のt分布の97.5%点、データが中心化されていない場合はdf = n - aのt分布の97.5%点とします。
個々の応答値に対する95%信頼区間は、次式で求められます。